题目内容
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0 时,有 ![]() .
.
(1)求证:f(x)在[﹣1,1]上为增函数;
(2)求不等式 ![]() 的解集;
的解集;
(3)若 ![]() 对所有
对所有 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
【答案】
(1)解:证明:任取x1,x2∈[﹣1,1]且x1<x2,则 ![]() ,
,
∴f(x2)>f(x1),∴f(x)为增函数
(2)解: ![]() ,等价于
,等价于 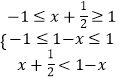 ,求得0≤x<
,求得0≤x< ![]() ,
,
即不等式 ![]() 的解集为
的解集为 ![]()
(3)解:由于f(x)为增函数,
∴f(x)的最大值为 ![]() 对
对 ![]() 恒成立
恒成立 ![]() 对
对 ![]() 的恒成立,
的恒成立,
设 ![]() ,则
,则 ![]() .
.
又 ![]() =
= ![]() =1+tan2α+2tanα+2=(tanα+1)2+2,
=1+tan2α+2tanα+2=(tanα+1)2+2,
∵α∈[﹣ ![]() ,
, ![]() ],∴tanα∈[﹣
],∴tanα∈[﹣ ![]() ,1],故当tanα=1时,
,1],故当tanα=1时,
![]()
∴t2+t≥6,求得t≤﹣3 t≥2,即为所求的实数t的取值范围.
【解析】(1)由条件利用增函数的定义证得结论.(2)根据函数的奇偶性和单调性,把要解的不等式等价转化为一个不等式组,求得此不等式的解集即可.(3)根据函数的单调性求得f(x)的最大值,可得t2+t≥g(α)= ![]() +2tanα+2 对
+2tanα+2 对 ![]() 的恒成立,再求得g(α)的最大值,从而求得t的范围.
的恒成立,再求得g(α)的最大值,从而求得t的范围.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值),还要掌握函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇)的相关知识才是答题的关键.

练习册系列答案
相关题目