题目内容
设等差数列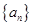 的前n项和为
的前n项和为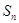 ,且满足条件
,且满足条件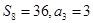
(1)求数列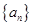 的通项公式;
的通项公式;
(2)令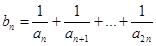 ,若对任意正整数
,若对任意正整数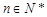 ,
, 恒成立,求
恒成立,求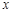 的取值范围.
的取值范围.
(1)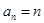 (2)
(2)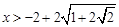 或
或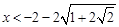
解析试题分析:(1))设等差数列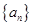 的首项为
的首项为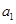 ,公差为d,利用
,公差为d,利用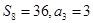 解出
解出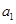 与d,最后求出数列
与d,最后求出数列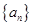 的通项公式;(2)先利用已知条件证明
的通项公式;(2)先利用已知条件证明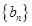 为递减数列,然后再借助于
为递减数列,然后再借助于 恒成立得到
恒成立得到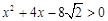 ,进而求出
,进而求出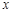 的取值范围.
的取值范围.
试题解析:(1)设 ,则
,则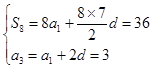 解得:
解得: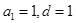 ∴
∴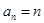
(2)∵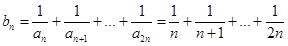
∴

∴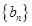 为递减数列 ∴
为递减数列 ∴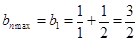
∵ 恒成立,∴
恒成立,∴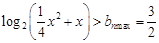
∴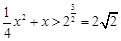 ∴
∴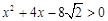
解得: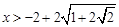 或
或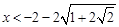
考点:等差数列的通项公式;递减数列;不等式恒成立的问题.

练习册系列答案
相关题目
 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列. 的前n项和为
的前n项和为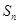 ,若
,若 ,求实数
,求实数 的值.
的值.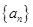 的通项公式为
的通项公式为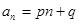 ,其中
,其中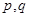 是常数,且
是常数,且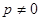 .
.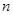 项和为
项和为 ,且
,且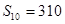 ,
,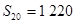 ,试确定
,试确定 的公式.
的公式. 为等差数列,且
为等差数列,且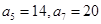 ,数列
,数列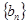 的前
的前 项和为
项和为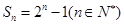 ,
,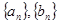 的通项公式;
的通项公式;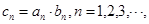 ,求数列
,求数列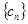 的前
的前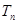 .
.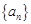 中,
中,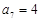 ,
,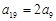 .
.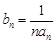 ,求数列
,求数列 的前
的前 项和
项和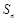 .
. 的前
的前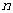 项和为
项和为 ,且
,且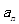 是
是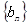 满足
满足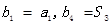 .
.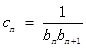 ,数列
,数列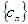 的前n项和为
的前n项和为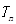 ,若
,若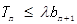 对一切
对一切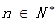 恒成立,求实数
恒成立,求实数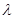 的最小值.
的最小值.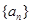 的公差为
的公差为 ,点
,点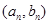 在函数
在函数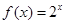 的图象上(
的图象上( ).
).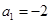 ,点
,点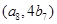 在函数
在函数 的图象上,求数列
的图象上,求数列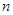 项和
项和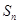 ;
;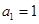 ,学科网函数
,学科网函数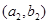 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列
,求数列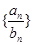 的前
的前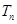 .
.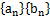 (
(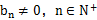 ),满足
),满足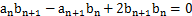 .
.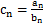 ,求数列
,求数列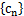 的通项公式;
的通项公式;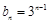 ,求数列
,求数列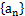 的前n项和
的前n项和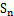
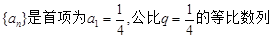 ,设数列
,设数列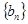 满足
满足 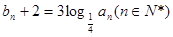 .
.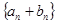 的前
的前 项和为
项和为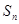 ;
; ,若
,若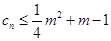 对一切正整数
对一切正整数 的取值范围.
的取值范围.