题目内容
设数列 为等差数列,且
为等差数列,且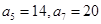 ,数列
,数列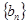 的前
的前 项和为
项和为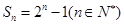 ,
,
(1)求数列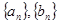 的通项公式;
的通项公式;
(2)若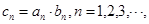 ,求数列
,求数列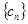 的前
的前 项和
项和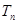 .
.
解析试题分析: (1)由等差数列的通项公式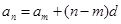 求公差
求公差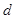 ,即可求
,即可求 ;利用
;利用 ,求
,求 ;(2)
;(2) 是等差数列,
是等差数列,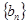 是等比数列,
是等比数列,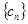 是由两者相乘,
是由两者相乘,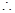 利用错位相减法求和即可.规律总结:1.等差数列的求解问题,要抓住五个基本量(
利用错位相减法求和即可.规律总结:1.等差数列的求解问题,要抓住五个基本量(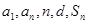 ),一般题型是“知三求二”,利用方程思想(关于
),一般题型是“知三求二”,利用方程思想(关于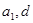 的方程)进行求有关量;2对于
的方程)进行求有关量;2对于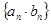 (其中
(其中 是等差数列,
是等差数列,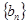 是等比数列)的求和问题,要利用错位相减法(乘公比
是等比数列)的求和问题,要利用错位相减法(乘公比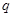 后,错位相减).
后,错位相减).
注意点:错位相减法,一定要向后错一位,使同次数的项对齐,以便正确化简;一定要搞清相减后,有多少项可构成等比数列.
试题解析: 是等差数列,
是等差数列,

 ,
,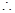 当
当 时,
时,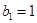 ;当
;当 时,
时,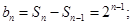
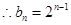 .
.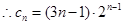
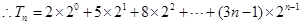
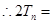
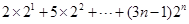
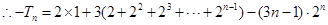
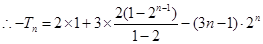

考点:1.等差数列;2.等比数列;3.错位相减法求数列的前 项和.
项和.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
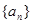 ,满足
,满足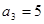 且
且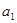 ,
,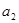 ,
,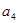 成等比数列.
成等比数列.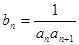 ,求数列
,求数列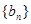 前
前 项的和为
项的和为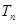 .
. 的前
的前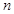 项和记为
项和记为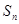 .已知
.已知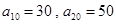 ,
,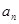 ;(2)若
;(2)若 ,求
,求 的前n项和为
的前n项和为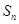 ,若
,若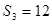 ,且
,且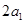 ,
,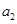 ,
,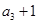 成等比数列,
成等比数列,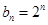 ,求数列
,求数列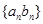 的前n项和
的前n项和 是首项
是首项 的递增等差数列,
的递增等差数列,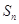 为其前
为其前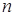 项和,且
项和,且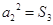 .
.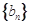 满足
满足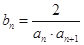 ,
,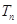 为数列
为数列 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.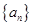 的前n项和为
的前n项和为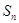 ,且满足条件
,且满足条件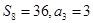
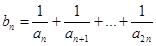 ,若对任意正整数
,若对任意正整数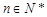 ,
, 恒成立,求
恒成立,求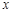 的取值范围.
的取值范围.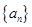 是递增的等差数列,
是递增的等差数列, ,
,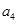 是方程
是方程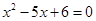 的根。
的根。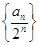 的前
的前 项和.
项和.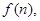 试写出
试写出 的表达式;
的表达式;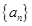 为等差数列,
为等差数列,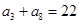 ,
,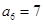 ,则
,则 ____________
____________