题目内容
函数
的最大值是（ ）A．1
B．
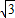
C．
D．2
【答案】分析：利用辅角公式与两角差的正弦公式对函数解析式进行化简可得y=2sin（x-
），再结合正弦函数的性质得到答案．
解答：解：由题意可得：
=2sin（x-
）
由正弦函数的性质可得：-1≤sin（x-
）≤1
∴-2≤f（x）≤2
∴函数
的最大值是2．
故选D．
点评：本题主要考查了正弦函数的定义域和值域，以及考查利用辅角公式与两角差的正弦公式对函数解析式的化简，此题属于基础题．
），再结合正弦函数的性质得到答案．解答：解：由题意可得：
=2sin（x-）由正弦函数的性质可得：-1≤sin（x-
）≤1∴-2≤f（x）≤2
∴函数
的最大值是2．故选D．
点评：本题主要考查了正弦函数的定义域和值域，以及考查利用辅角公式与两角差的正弦公式对函数解析式的化简，此题属于基础题．
练习册系列答案
相关题目
已知二次函数y=ax2+（a2+1）x在x=1处的导数值为1，则该函数的最大值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|