题目内容
(本小题14分) 如图,在平面直角坐标系xoy中,设点F(0, p)(p>0), 直线l : y= -p, 点P在直线l上移动,R是线段PF与x轴的交点, 过R、P分别作直线 、
、 ,使
,使 ,
,
 .
.
(1)求动点Q的轨迹C的方程;
(2)在直线l上任取一点M做曲线C的两条切线,设切点为A、B,求证:直线AB恒过一定点;
(3)对(2)求证:当直线MA, MF, MB的斜率存在时,直线MA, MF, MB的斜率的倒数成等差数列.
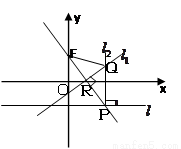
(1) .(2)直线恒过定点
.(2)直线恒过定点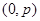 .
(3) 证明:见解析。
.
(3) 证明:见解析。
【解析】
试题分析:(Ⅰ)先判断RQ是线段FP的垂直平分线,从而可得动点Q的轨迹C是以F为焦点,l为准线的抛物线;
(Ⅱ)设M(m,-p),两切点为A(x1,y1),B(x2,y2),求出切线方程,从而可得x1,x2为方程x2-2mx-4p2=0的两根,进一步可得直线AB的方程,即可得到直线恒过定点(0,p);
(Ⅲ) 由(Ⅱ)的结论,设M(m,-p),A(x1,y1),B(x2,y2),且有x1+x2=2m,x1x2=-4p2,从而可得kMA ,kMB由此可证直线MA,MF,MB的斜率的倒数成等差数列.
解:(1)依题意知,点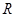 是线段
是线段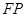 的中点,且
的中点,且 ⊥
⊥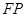 ,
,
∴ 是线段
是线段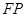 的垂直平分线. ∴
的垂直平分线. ∴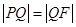 .
.
故动点 的轨迹
的轨迹 是以
是以 为焦点,
为焦点,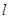 为准线的抛物线,
为准线的抛物线,
其方程为: .
.
(2)设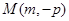 ,两切点为
,两切点为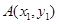 ,
,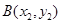
∴两条切线方程为x x=2p(y+y
x=2p(y+y )
①
)
①
x x=2p(y+y
x=2p(y+y ) ②
) ②
对于方程①,代入点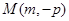 ,
又
,
又 , 整理得:
, 整理得: ,
同理对方程②有
,
同理对方程②有 ,
即
,
即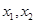 为方程
为方程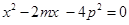 的两根.
的两根.
∴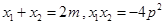 ③
③
设直线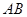 的斜率为
的斜率为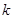 ,
,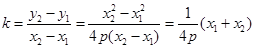
所以直线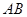 的方程为
的方程为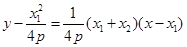 ,展开得:
,展开得: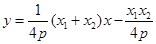 ,代入③得:
,代入③得: ,
∴直线恒过定点
,
∴直线恒过定点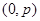 .
.
(3) 证明:由(2)的结论,设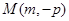 ,
,
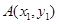 ,
,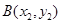
且有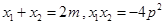 ,
,
∴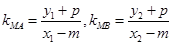
∴

=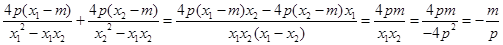
又∵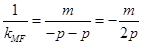 ,所以
,所以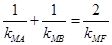
即直线 的斜率倒数成等差数列.
的斜率倒数成等差数列.
考点:本题主要考查了抛物线的定义,考查直线恒过定点,考查直线的向量。属于中档题
点评:解决该试题的关键是正确运用韦达定理,以及抛物线中x,y关系式的转化与化简是解决试题的又一个难点。

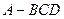 中,
中,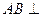 平面
平面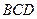 ,
,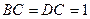 ,
,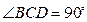 ,
,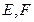 分别是
分别是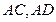 上
上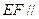 平面
平面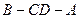 为
为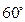 .
.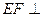 平面
平面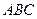 ;
;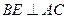 ,求直线
,求直线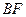 与平面
与平面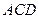 所成角的余弦值.
所成角的余弦值.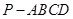 中,底面
中,底面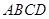 为矩形,侧棱
为矩形,侧棱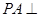 底面
底面 为
为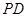 的中点.
的中点.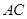 与
与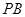 所成角的余弦值;
所成角的余弦值;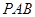 内找一点
内找一点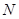 ,使
,使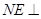 平面
平面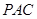 ,并分别求出点
,并分别求出点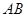 和
和 的距离.
的距离.
 中,
中, ,点
,点 在边
在边 上,
上, 。
。 平面
平面 ;
; 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.
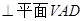 ;
;