题目内容
7.已知点P(a+b,a-b)在不等式组$\left\{{\begin{array}{l}{x-2y+2≥0}\\{y≥|x|}\end{array}}\right.$表示的区域内,则2a+b的最大值为( )| A. | $-\frac{2}{3}$ | B. | 0 | C. | 4 | D. | 6 |
分析 利用换元法,转化a、b为x,y的关系,利用线性规划求解目标函数的最值即可.
解答 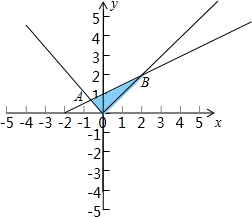 解:令x=a+b,y=a-b,则2a+b=$\frac{3}{2}x+\frac{1}{2}y$,
解:令x=a+b,y=a-b,则2a+b=$\frac{3}{2}x+\frac{1}{2}y$,
画出不等式组$\left\{{\begin{array}{l}{x-2y+2≥0}\\{y≥|x|}\end{array}}\right.$的可行域,
$\frac{3}{2}x+\frac{1}{2}y$在点B处,取得最大值,
由$\left\{\begin{array}{l}x-2y+2=0\\ y=x\end{array}\right.$,可得$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$,即B(2,2),
2a+b的最大值为$\frac{3}{2}x+\frac{1}{2}y$在点B处的最大值为:4.
故选:C.
点评 本题考查线性规划的应用,作出可行域以及判断目标函数的最值是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.设复数z=1+i(i是虚数单位),则|$\frac{2}{z}$+z2|=( )
| A. | 1+i | B. | -1+i | C. | $\sqrt{2}$ | D. | 2 |
15.△ABC中,角A,B,C所对边的长分别为a,b,c,满足a2+b2=2c2,则cosC的最小值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
2.设实数x,y满足不等式组$\left\{{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥-1}\end{array}}\right.$.则z=3x+y的取值范围是( )
| A. | [-4,0] | B. | [0,4] | C. | [-2,4] | D. | [-4,4] |
12.已知A={x|1<x≤3},B={y|y=($\frac{1}{2}$)x-2,x∈A},则(∁RA)∩B=( )
| A. | (0,1] | B. | (0,1]∪(3,+∞) | C. | (1,3] | D. | $[\frac{1}{2}{,^{\;}}1]$ |
19.在△ABC中,角A,B,C的对边为a,b,c,b=8,c=8$\sqrt{3}$,S△ABC=16$\sqrt{3}$,则A等于( )
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
16.在△ABC中,a,b,c分别为角A,B,C的对边,若cos2$\frac{B}{2}=\frac{a+c}{2c}$,则△ABC的形状为( )
| A. | 正三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰三角形或直角三角形 |