题目内容
8.已知数列{an}的前n项和Sn 满足:Sn=(-1)n+1n,求an.分析 通过分n为奇数、偶数两种情况讨论,利用an=Sn-Sn-1计算即得结论.
解答 解:依题意,当n=2k-1时Sn=n,当n=2k时Sn=-n,
∴当n=2k-1时an=Sn-Sn-1=n+n-1=2n-1;
当n=2k时,an=Sn-Sn-1=-n-(n-1)=-(2n-1);
综上所述,an=(-1)n+1(2n-1).
点评 本题考查数列的通项,考查分类讨论的思想,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
19.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1与直线y=2x有公共点与y=3x没有公共点,则双曲线的离心率的取值范围为( )
| A. | ($\sqrt{5}$,$\sqrt{10}$] | B. | (1,$\sqrt{10}$] | C. | (1,$\sqrt{5}$] | D. | [$\sqrt{5}$,+∞) |
16.已知集合A={y|y=log${\;}_{\frac{1}{2}}$x,0<x<1},B={y|y=2x,x<0].则A∩B等于( )
| A. | {y|0<y<$\frac{1}{2}$} | B. | {y|0<y<1} | C. | {y|$\frac{1}{2}$<y<1} | D. | ∅ |
17.设复数z=1+i(i是虚数单位),则|$\frac{2}{z}$+z2|=( )
| A. | 1+i | B. | -1+i | C. | $\sqrt{2}$ | D. | 2 |
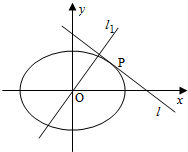 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.