题目内容
已知f(x)为R上的可导函数,且对?x∈R,均有f(x)>f'(x),则有
- A.e2013f(-2013)<f(0),f(2013)<e2013f(0)
- B.e2013f(-2013)<f(0),f(2013)>e2013f(0)
- C.e2013f(-2013)>f(0),f(2013)<e2013f(0)
- D.e2013f(-2013)>f(0),f(2013)>e2013f(0)
C
分析:根据题目给出的条件:“f(x)为R上的可导函数,且对?x∈R,均有f(x)>f'(x)”,结合给出的四个选项,设想寻找一个辅助函数g(x)=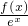 ,
,
这样有以e为底数的幂出现,求出函数g(x)的导函数,由已知得该导函数大于0,得出函数g(x)为减函数,利用函数的单调性即可得到结论.
解答:令 ,则
,则 ,
,
因为f(x)>f'(x),所以g′(x)<0,所以函数g(x)为R上的减函数,
所以g(-2013)>g(0),
即 ,所以e2013f(-2013)>f(0),
,所以e2013f(-2013)>f(0),
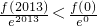 ,所以f(2013)<e2013f(0).
,所以f(2013)<e2013f(0).
故选C.
点评:本题考查了导数的运算,由题目给出的条件结合选项去分析函数解析式,属逆向思维,属中档题.
分析:根据题目给出的条件:“f(x)为R上的可导函数,且对?x∈R,均有f(x)>f'(x)”,结合给出的四个选项,设想寻找一个辅助函数g(x)=
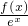 ,
,这样有以e为底数的幂出现,求出函数g(x)的导函数,由已知得该导函数大于0,得出函数g(x)为减函数,利用函数的单调性即可得到结论.
解答:令
 ,则
,则 ,
,因为f(x)>f'(x),所以g′(x)<0,所以函数g(x)为R上的减函数,
所以g(-2013)>g(0),
即
 ,所以e2013f(-2013)>f(0),
,所以e2013f(-2013)>f(0),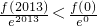 ,所以f(2013)<e2013f(0).
,所以f(2013)<e2013f(0).故选C.
点评:本题考查了导数的运算,由题目给出的条件结合选项去分析函数解析式,属逆向思维,属中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知f(x)为R上的减函数,则满足f(
)>f(1)的实数x的取值范围是( )
| 1 |
| x |
| A、(-∞,1) |
| B、(1,+∞) |
| C、(-∞,0)∪(0,1) |
| D、(-∞,0)∪(1,+∞) |
已知 f(x)为R上的可导函数,且f(x)<f'(x)和f(x)>0对于x∈R恒成立,则有( )
| A、f(2)<e2-f(0),f(2010)>e2010-f(0) | B、f(2)>e2-f(0),f(2010)>e2010-f(0) | C、f(2)<e2-f(0),f(2010)<e2010-f(0) | D、f(2)<e2-f(0),f(2010)<e2010-f(0) |