题目内容
设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
(1)当 时,
时, 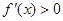 ,函数
,函数 在定义域
在定义域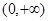 上单调递增
上单调递增
(2)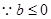 时,
时, 有惟一极小值点
有惟一极小值点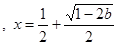 ,
,
(3)由(2)可知当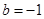 时,函数
时,函数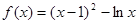 ,此时
,此时 有惟一极小值点
有惟一极小值点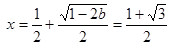 故可以得到函数
故可以得到函数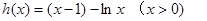 借助于单调性来证明不等式。
借助于单调性来证明不等式。
解析试题分析:解:(1)由题意知, 的定义域为
的定义域为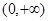 ,
,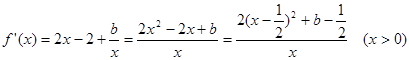
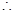 当
当 时,
时, 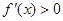 ,函数
,函数 在定义域
在定义域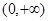 上单调递增. …………4分
上单调递增. …………4分
(2)当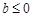 时
时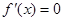 有两个不同解,
有两个不同解,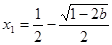
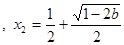
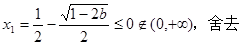 ,
,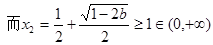 ,
,
此时 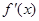 ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
由此表可知:
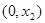
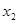
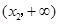
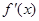
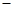

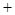

减 极小值 增 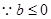 时,
时, 有惟一极小值点
有惟一极小值点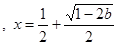 , ………8分
, ………8分
(3)由(2)可知当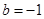 时,函数
时,函数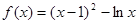 ,
,
此时 有惟一极小值点
有惟一极小值点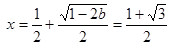
且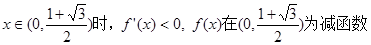
 …… 11分
…… 11分
令函数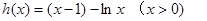
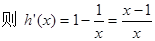
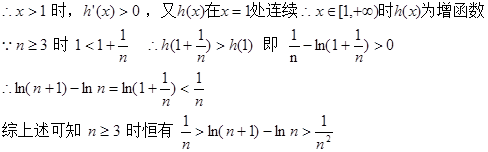 13分
13分
考点:导数的运用
点评:主要是考查了导数在研究函数中的运用,以及函数的极值,以及函数与不等式的综合运用,属于难度题。

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”.
为“一阶比增函数”.
(Ⅰ) 若 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数 的取值范围;
的取值范围;
(Ⅱ) 若 是“一阶比增函数”,求证:
是“一阶比增函数”,求证: ,
, ;
;
(Ⅲ)若 是“一阶比增函数”,且
是“一阶比增函数”,且 有零点,求证:
有零点,求证: 有解.
有解.
探究函数f(x)=x+ ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;(1)函数f(x)=x+
 (x>0)在区间 上递增.
(x>0)在区间 上递增.当x= 时,y最小= .
(2)证明:函数f(x)=x+
 在区间(0,2)上递减.
在区间(0,2)上递减.(3)思考:函数f(x)=x+
 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)  ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 ,试判断
,试判断 是定义在区间
是定义在区间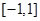 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 ,
,
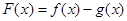 的单调区间;
的单调区间; 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 满足
满足 .求证:
.求证: .
. .
. 的单调区间;
的单调区间; 时
时 恒成立,求
恒成立,求 的取值范围。
的取值范围。 ,函数
,函数 ,其中
,其中 是自然对数的底数。
是自然对数的底数。 在R上的单调性;
在R上的单调性; 时,求
时,求 上的最值。
上的最值。 满足
满足 ,其中a>0,a≠1.
,其中a>0,a≠1.
 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。 .
.  处取到极值?若有可能,求实数
处取到极值?若有可能,求实数 的值;否则说明理由;
的值;否则说明理由; 上为增函数,求实数
上为增函数,求实数