题目内容
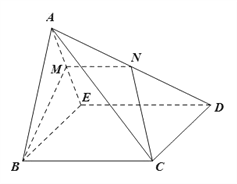
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(Ⅰ)证明![]() 即可得到
即可得到![]() 平面
平面![]()
(Ⅱ)证明![]() 和
和![]() 即可证明
即可证明![]() 平面
平面![]()
(Ⅲ)取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,过
,过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() . 则点
. 则点![]() 即为所求作的点.
即为所求作的点.
试题解析:(Ⅰ)因为点![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,所以
的中点,所以![]()
因为四边形为正方形,所以![]()
所以![]()
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)因为平面![]() 底面
底面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]()
因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅲ)取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,过
,过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() . 则点
. 则点![]() 即为所求作的点.
即为所求作的点.
理由:因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]()
因为平面![]() 底面
底面![]() ,所以
,所以![]() 平面
平面![]()
所以![]()
![]()
因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]()
![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目