题目内容
长方体
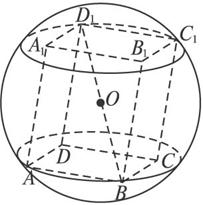
![]() 解析:设球的半径为R,由题目知,长方体ABCD—A1B1C1D1内接于球.
解析:设球的半径为R,由题目知,长方体ABCD—A1B1C1D1内接于球.
此时长方体的体对角线即为球的直径,长方体的中心即为球心,所以BD1=2R,由AB∶AD∶AA1=1∶1∶![]() ,
,
设AB=k,AD=k,AA1=![]() k,
k,
所以有BD1=![]() =2k=2R,
=2k=2R,
因此k=R,所以AB=R,AD=R,AA1=![]() R,得∠AOB=
R,得∠AOB=![]() ,∠AOD1=
,∠AOD1=![]() ,
,
由球面距离的定义,扇形AOB的弧![]() 即为AB的球面距离.
即为AB的球面距离.
因此![]() =
=![]() ·R;同理扇形AOD1的弧
·R;同理扇形AOD1的弧![]() 为AD1的球面距离.
为AD1的球面距离.
因此![]() =
=![]() ·R,∴
·R,∴![]() =
=![]() =
=![]() =
=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目