题目内容
长方体的长、宽、高分别为3、2、1,若该长方体的各顶点都在球O的表面上,则球O的表面积为
14π
14π
.分析:通过长方体的各顶点都在球O的表面上,求出长方体的对角线的长度就是外接球的直径,求出直径,即可求解球O的表面积.
解答:解:因为长方体的各顶点都在球O的表面上,长方体的对角线的长度就是外接球的直径,
又长方体的长、宽、高分别为3、2、1,所以长方体的对角线长度为:
=
所以球的半径为:
所以球O的表面积4π×
=14π
故答案为:14π.
又长方体的长、宽、高分别为3、2、1,所以长方体的对角线长度为:
| 32+22+12 |
| 14 |
所以球的半径为:
| ||
| 2 |
所以球O的表面积4π×
| 14 |
| 4 |
故答案为:14π.
点评:本题考查球的内接多面体,球的表面积的求法,解题的关键是确定长方体的对角线的长度就是外接球的直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

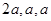 ,其顶点都在一个球面上,则该球的表面积为( )
,其顶点都在一个球面上,则该球的表面积为( ) B.
B.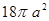 C.
C. D.
D.
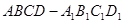 的长,宽,高分别是3,2,1,则该长方体的体对角线是( )
的长,宽,高分别是3,2,1,则该长方体的体对角线是( )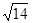 B.
B.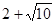 C.
C. D.
D.