题目内容
(2008•海珠区一模)已知点A(1+sin(
-2x),1),B(1,
sin(π-2x)+a)(x∈R,a),y=
•
.
(1)求y关于x的函数关系式y=f(x);
(2)当x∈[0,
]时f(x)的最大值为4,求a的值.
| π |
| 2 |
| 3 |
| OA |
| OB |
(1)求y关于x的函数关系式y=f(x);
(2)当x∈[0,
| π |
| 3 |
分析:(1)利用两个向量的数量积公式,两角和的正弦公式,化简f(x)的解析式为2sin(
+2x)+a+1.
(2)根据x的范围求出2x+
的范围,从而求出f(x)=2sin(
+2x)+a+1的最大值,再根据它的最大值等于4求出a的值
| π |
| 6 |
(2)根据x的范围求出2x+
| π |
| 6 |
| π |
| 6 |
解答:解:∵(1)点A(1+sin(
-2x),1),B(1,
sin(π-2x)+a)(a、x∈R,),
∴y=f(x)=
•
=(1+sin(
-2x),1)•(1,
sin(π-2x)+a)=1+cos2x+
sin2x+a=2sin(
+2x)+a+1
(2)当x∈[0,
]时,
≤2x+
≤
,故当2x+
=
时,函数y有最大值等于2+a+1=4,a=1.
| π |
| 2 |
| 3 |
∴y=f(x)=
| OA |
| OB |
| π |
| 2 |
| 3 |
| 3 |
| π |
| 6 |
(2)当x∈[0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 2 |
点评:本题主要考查两个向量的数量积公式,两角和的正弦公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
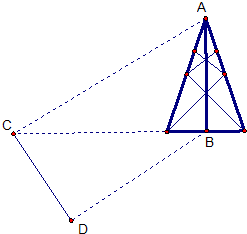 (2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.
(2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB. (2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )
(2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )