题目内容
【题目】设椭圆E: ![]() (a>b>0),其长轴长是短轴长的
(a>b>0),其长轴长是短轴长的 ![]() 倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2
倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2 ![]() .
.
(1)求椭圆E的方程;
(2)设过右焦点F2且与x轴不垂直的直线l交椭圆E于P,Q两点,在线段OF2(O为坐标原点)上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
【答案】
(1)解:不妨设焦点的坐标是(c,0),
则过焦点且垂直于x轴的直线与椭圆的交点坐标为(c,y0),
代入 ![]() 可得,y0=
可得,y0= ![]() ,
,
因为过焦点且垂直于x轴的直线被椭圆截得的弦长为2 ![]() ,
,
所以 ![]() ,
,
由题意得,a= ![]() b,代入上式解得:a=2
b,代入上式解得:a=2 ![]() 、b=
、b= ![]() ,
,
故所求椭圆方程为 ![]()
(2)解:假设在线段OF2上存在点M(m,0)( ![]() )满足条件,
)满足条件,
∵直线与x轴不垂直,
∴设直线l的方程为 ![]() .
.
设P(x1,y1),Q(x2,y2),
由 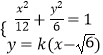 ,可得
,可得 ![]() .
.
则 ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() ,其中x2﹣x1≠0,
,其中x2﹣x1≠0,
∵以MP,MQ为邻边的平行四边形是菱形,
∴ ![]() .
.
∴(x1+x2﹣2m)(x2﹣x1)+(y1+y2)(y2﹣y1)=0.
∴x1+x2﹣2m+k(y1+y2)=0.
∴ ![]() .
.
化简得 ![]() =
= ![]() (k≠0),
(k≠0),
则 ![]()
在线段OF2上存在点M(m,0)符合条件,且 ![]()
【解析】(1)由题意先求出直线与椭圆的交点坐标,再列出方程求出a、b的值,代入椭圆方程即可;(2)先假设存在点M(m,0)( ![]() )满足条件,由点斜式设出直线l的方程,以及P、Q的坐标,将直线方程代入椭圆方程化简后,利用韦达定理、菱形的等价条件、向量知识,可求出m的范围,再进行判断.
)满足条件,由点斜式设出直线l的方程,以及P、Q的坐标,将直线方程代入椭圆方程化简后,利用韦达定理、菱形的等价条件、向量知识,可求出m的范围,再进行判断.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目