题目内容
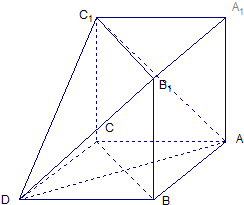 在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形.
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形.(1)求证:AD⊥平面BCC1B1
(2)求该多面体的体积.
分析:(1)通过证线线垂直⇒线面垂直即可.
(2)几何体是一个三棱柱与四棱锥的组合体,分别判定几何体的底面与高,根据公式求解即可.
(2)几何体是一个三棱柱与四棱锥的组合体,分别判定几何体的底面与高,根据公式求解即可.
解答:解:(1)证明:∵正三棱柱ABC-A1B1C1,∴BB1⊥AD
∵四边形ABDC是菱形,∴AD⊥BC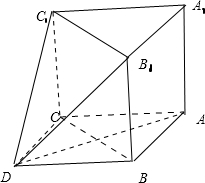
又BB1,BC?平面BB1C1C,且BC∩BB1=B
∴AD⊥平面BCC1B1
(2)正三棱柱ABC-A1B1C1的体积为V棱柱=S△ABC×AA1=
×2×2×
×2=2
;
∵AD⊥平面BCC1B1,∴四棱锥D-B1C1CB的高为
AD
∴四棱锥D-B1C1CB的体积为V棱锥=
×2×2×
=
∴该多面体的体积V=V棱锥+V棱柱=
.
∵四边形ABDC是菱形,∴AD⊥BC

又BB1,BC?平面BB1C1C,且BC∩BB1=B
∴AD⊥平面BCC1B1
(2)正三棱柱ABC-A1B1C1的体积为V棱柱=S△ABC×AA1=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵AD⊥平面BCC1B1,∴四棱锥D-B1C1CB的高为
| 1 |
| 2 |
∴四棱锥D-B1C1CB的体积为V棱锥=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
∴该多面体的体积V=V棱锥+V棱柱=
| 10 |
| 3 |
| 3 |
点评:本题考查线面垂直的判定与空间几何体的体积.V椎体=
Sh,V柱体=Sh.
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
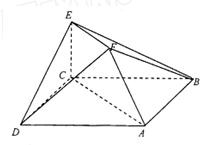
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=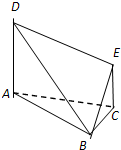 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.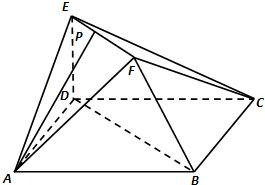 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和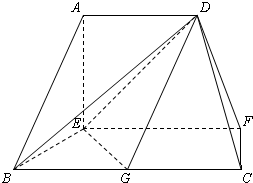 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.