题目内容
 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.(1)求证:BD⊥EG;
(2)求平面DEG与平面DEF所成锐二面角的余弦值.
分析:解法1
(1)证明BD⊥EG,只需证明EG⊥平面BHD,证明DH⊥EG,BH⊥EG即可;
(2)先证明∠GMH是二面角G-DE-F的平面角,再在△GMH中,利用余弦定理,可求平面DEG与平面DEF所成锐二面角的余弦值;
解法2
(1)证明EB,EF,EA两两垂直,以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立空间直角坐标系用坐标表示点与向量,证明
•
=0,可得BD⊥EG;
(2)由已知得
=(2,0,0)是平面DEF的法向量,求出平面DEG的法向量
=(1,-1,1),利用向量的夹角公式,可求平面DEG与平面DEF所成锐二面角的余弦值.
(1)证明BD⊥EG,只需证明EG⊥平面BHD,证明DH⊥EG,BH⊥EG即可;
(2)先证明∠GMH是二面角G-DE-F的平面角,再在△GMH中,利用余弦定理,可求平面DEG与平面DEF所成锐二面角的余弦值;
解法2
(1)证明EB,EF,EA两两垂直,以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立空间直角坐标系用坐标表示点与向量,证明
| BD |
| EG |
(2)由已知得
| EB |
| n |
解答: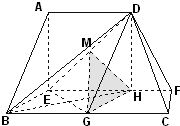 解法1
解法1
(1)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,
∴AE⊥平面BCFE.…(2分)
过D作DH∥AE交EF于H,则DH⊥平面BCFE.
∵EG?平面BCFE,
∴DH⊥EG.…(4分)
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,
∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,
∴BH⊥EG,…(6分)
又BH∩DH=H,BH?平面BHD,DH?平面BHD,
∴EG⊥平面BHD.…(7分)
∵BD?平面BHD,
∴BD⊥EG.…(8分)
(2)解:∵AE⊥平面BCFE,AE?平面AEFD,∴平面AEFD⊥平面BCFE
由(1)可知GH⊥EF,∴GH⊥平面AEFD
∵DE?平面AEFD,∴GH⊥DE…(9分)
取DE的中点M,连接MH,MG
∵四边形AEHD是正方形,∴MH⊥DE
∵MH∩GH=H,MH?平面GHM,GH?平面GHM,∴DE⊥平面GHM,∴DE⊥MG
∴∠GMH是二面角G-DE-F的平面角,…(12分)
在△GMH中,GH=2,MH=
,MG=
,∴cos∠GMH=
=
…(13分)
∴平面DEG与平面DEF所成锐二面角的余弦值为
.…(14分)
解法2
(1)证明:∵EF⊥平面AEB,AE?平面AEB,BE?平面AEB,∴EF⊥AE,EF⊥BE,
又AE⊥EB,∴EB,EF,EA两两垂直.…(2分)
以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立如图所示的空间直角坐标系.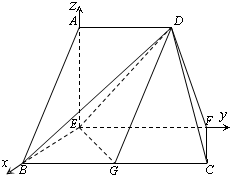
由已知得,A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0).…(4分)
∴
=(2,2,0),
=(-2,2,2),…(6分)
∴
•
=-2×2+2×2=0,…(7分)
∴BD⊥EG.…(8分)
(2)解:由已知得
=(2,0,0)是平面DEF的法向量.…(9分)
设平面DEG的法向量为
=(x,y,z),
∵
=(0,2,2),
=(2,2,0),
∴
,即
,令x=1,得
=(1,-1,1).…(12分)
设平面DEG与平面DEF所成锐二面角的大小为θ,
则cosθ=|cos<
,
>|=
=
=
…(13分)
∴平面DEG与平面DEF所成锐二面角的余弦值为
.…(14分)
 解法1
解法1(1)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,
∴AE⊥平面BCFE.…(2分)
过D作DH∥AE交EF于H,则DH⊥平面BCFE.
∵EG?平面BCFE,
∴DH⊥EG.…(4分)
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,
∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,
∴BH⊥EG,…(6分)
又BH∩DH=H,BH?平面BHD,DH?平面BHD,
∴EG⊥平面BHD.…(7分)
∵BD?平面BHD,
∴BD⊥EG.…(8分)
(2)解:∵AE⊥平面BCFE,AE?平面AEFD,∴平面AEFD⊥平面BCFE
由(1)可知GH⊥EF,∴GH⊥平面AEFD
∵DE?平面AEFD,∴GH⊥DE…(9分)
取DE的中点M,连接MH,MG
∵四边形AEHD是正方形,∴MH⊥DE
∵MH∩GH=H,MH?平面GHM,GH?平面GHM,∴DE⊥平面GHM,∴DE⊥MG
∴∠GMH是二面角G-DE-F的平面角,…(12分)
在△GMH中,GH=2,MH=
| 2 |
| 6 |
| ||
|
| ||
| 3 |
∴平面DEG与平面DEF所成锐二面角的余弦值为
| ||
| 3 |
解法2
(1)证明:∵EF⊥平面AEB,AE?平面AEB,BE?平面AEB,∴EF⊥AE,EF⊥BE,
又AE⊥EB,∴EB,EF,EA两两垂直.…(2分)
以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立如图所示的空间直角坐标系.

由已知得,A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0).…(4分)
∴
| EG |
| BD |
∴
| BD |
| EG |
∴BD⊥EG.…(8分)
(2)解:由已知得
| EB |
设平面DEG的法向量为
| n |
∵
| ED |
| EG |
∴
|
|
| n |
设平面DEG与平面DEF所成锐二面角的大小为θ,
则cosθ=|cos<
| n |
| EB |
|
| ||||
|
|
| 2 | ||
2
|
| ||
| 3 |
∴平面DEG与平面DEF所成锐二面角的余弦值为
| ||
| 3 |
点评:本题考查线线垂直,考查面面角,考查利用空间向量解决立体几何问题,两法并举,注意体会.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目