Question

【题目】数列的前项和为，且

（1）求数列的通项公式；

（2）若数列满足：，求 的通项公式；

（3）令，求数列的前项和.

Answer 1

【答案】(1) .

(2)

(3) 故数列的前项和为

【解析】分析：（1）知道，求数列的通项公式，应用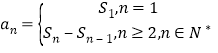来解。由得，两式相减得。根据，求得 。满足上式。进而可得。(2)由可得。两式相减可得，变形可得，进而可得 （3）由以和 可得。

根据数列的通项公式得特点，可用分组求和得数列的前项和为，对于求，是等差数列和等比数列的对应项乘积的和，故可用错位相减法求和得。对于求，可用等差数列的求和公式。故数列的前项和为

详解：（1）由得，

两式相减得，

对于，当时， 。满足上式。

所以

（2），

，

两式相减得

所以。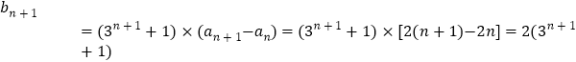

于是：

(3)

令

则

两式相减得

，

故数列的前项和为