题目内容
【题目】已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,公差
,公差![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() ;数列
;数列![]() 满足:对于任意的
满足:对于任意的![]() ,等式
,等式![]() 都成立.
都成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 满足
满足![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有满足条件的数组
成等比数列?若存在,求出所有满足条件的数组![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1) ![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】分析:(1)根据已知解方程组得![]() ,即得数列
,即得数列![]() 的通项公式.(2)利用作差法化简
的通项公式.(2)利用作差法化简
![]() 即得
即得![]() ,即证明数列
,即证明数列![]() 是等比数列.(3)先化简
是等比数列.(3)先化简![]() ,再化简
,再化简![]() ,
,![]() ,
,![]() 成等比数列,对s分类讨论得解.
成等比数列,对s分类讨论得解.
详解:(1)设数列![]() 公差为
公差为![]() ,由题设得
,由题设得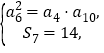
即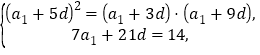 解得
解得![]()
∴数列![]() 的通项公式为:
的通项公式为:![]() .
.
(2)∵![]()
∴![]() ,①
,①
∴![]() ,②
,②
由②-①得![]() ,③
,③
∴![]() ,④
,④
由④-③得![]() ,
,
由①知![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴数列
,∴数列![]() 是等比数列.
是等比数列.
(3)假设存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
由(2)可知:![]() ,∴
,∴![]() .
.
于是,![]() .
.
由于![]() ,所以
,所以![]()
因为当![]() 时,
时,![]() ,即
,即![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() ,不符合条件,
,不符合条件,
所以![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]()
当![]() 时,得
时,得![]() ,无解,
,无解,
当![]() 时,得
时,得![]() ,所以
,所以![]() ,
,
综上:存在唯一正整数数组![]() ,使
,使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.

练习册系列答案
相关题目
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
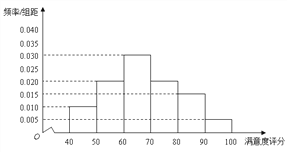
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由



