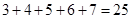题目内容
若△ABC的三边之长分别为a、b、c，内切圆半径为r，则△ABC的面积为 
．根
据类比思想可得：若四面体A-BCD的三个侧面与底面的面积分别为
，内切球的半径为r，则四面体的体积为（ ）
．根据类比思想可得：若四面体A-BCD的三个侧面与底面的面积分别为，内切球的半径为r，则四面体的体积为（ ）A． | B． | C． | D． |
A
试题分析：根据三角形的边应与四面体中的各个面进行类比，而面积与体积进行类比，进行猜想. 解：根据几何体和平面图形的类比关系，三角形的边应与四面体中的各个面进行类比，而面积与体积进行类比：∴△ABC的面积为
，对应于四面体的体积为，故选A点评：本题考察了立体几何和平面几何的类比推理，一般平面图形的边、面积分别于几何体中的面和体积进行类比，从而得到结论
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
是减函数（大前提），而y=
是对数函数（小前提），所以y=
，则按此规律可猜想第n个不等式为 .
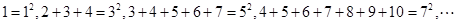，得出的一般性结论为________________________
,
,
,
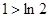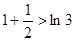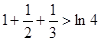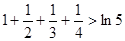, ,则可以归纳出第
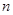个式子为 
五个方面的多元评价指标，并通过经验公式
来计算各班的综合得分，
的值越高则评价效果越好．若某班在自测过程中各项指标显示出
，则下阶段要把其中一个指标的值增加
个单位，而使得
