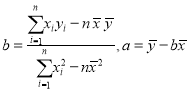题目内容
【题目】某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须整改.若整改后经复查仍不合格,则强制关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8.计算(结果精确到0.01):
(1)恰好有两家煤矿必须整改的概率.
(2)平均有多少家煤矿必须整改?
(3)至少关闭一家煤矿的概率.
【答案】(1) P1
0.31.
（2）2.50家.
（3）P3≈0.41.
【解析】分析：（1）由
次独立重复试验的概率公式计算（本题是5次独立重复试验恰好发生2次的概率；
（2）必须整改的煤矿数服从二项分布
，由此可得期望；
（3）某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格，由独立事件同时发生的概率公式可得．
详解：根据独立重复试验与相互独立事件的概率求解.
(1)每家煤矿必须整改的概率是(1-0.5),且每家煤矿是否整改是相互独立的.
所以恰好有两家煤矿必须整改的概率是
P1=
(1-0.5)2×0.53=
0.31.
(2)由题设,必须整改的煤矿数X服从二项分布B(5,0.5),从而X的数学期望是E(X)=5×0.5=2.5,即平均有2.50家煤矿必须整改.
(3)某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是
P2=(1-0.5)×(1-0.8)=0.1.
从而该煤矿不被关闭的概率是0.9.
由题意,每家煤矿是否被关闭是相互独立的,故至少关闭一家煤矿的概率是P3=1-0.95≈0.41.
【题目】某生产企业研发了一种新产品，该产品在试销一个阶段后得到销售单价
（单位：元）和销售量
（单位：万件）之间的一组数据，如下表所示：
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
（1）根据表中数据，建立关于的线性回归方程；
（2）从反馈的信息来看，消费者对该产品的心理价（单位：元/件）在
内，已知该产品的成本是
元，那么在消费者对该产品的心理价的范围内，销售单价定为多少时，企业才能获得最大利润？（注：利润=销售收入-成本）
参考数据：
参考公式：
