题目内容
【题目】已知有穷数列
， 
， 
， 
， 
，若数列
中各项都是集合
的元素，则称该数列为
数列．
对于
数列
，定义如下操作过程
从
中任取两项
， 
，将
的值添在
的最后，然后删除
， 
，这样得到一个
项的新数列，记作
（约定：一个数也视作数列）．若
还是
数列，可继续实施操作过程
．得到的新数列记作
， 
，如此经过
次操作后得到的新数列记作
．
（Ⅰ）设
， 
， 
， 
，请写出
的所有可能的结果．
（Ⅱ）求证：对
数列
实施操作过程
后得到的数列
仍是
数列．
（Ⅲ）设
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，求
的所有可能的结果，并说明理由．
【答案】（
）见解析（
）见解析（
）
．
【解析】试题分析：（1）
中任取2项，有
种取法，所以可以得到6种
；（2）由
，有
，得证；（3）经验证，我们可知
数列满足交换律和结合律，与具体操作过程无关，则
，
易知
， 
， 
， 
．
，所以
．
试题解析：
（
）
有如下
种可知结果： 
， 
， 
； 
， 
， 
；
， 
， 
； 
， 
， 
； 
， 
， 
； 
， 
， 
．
（
）证明：∵
， 
，有：
且
，
∴
．
故对
数列实施操作
后得到的数列
仍是
数列．
（
）由题意可知
中仅有一项，
对于满足
， 
的实数
， 
定义运算： 
，
下面证明这种运算满足交换律和结合律．
∵
，且
，
∴
，即该运算满足交换律．
∵
，
．
∴
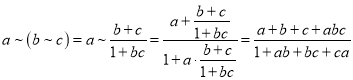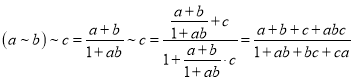，即该运算满足结合律，
∴
中的项与实施的具体操作过程无关．
选择如下操作过程求
，由（
）可知
，
易知
， 
， 
， 
．
．
综上可知
．
练习册系列答案
阅读快车系列答案
相关题目
