题目内容
5.已知$\overrightarrow{a}$=(x-1,y),$\overrightarrow{b}$=(x+1,y).|$\overrightarrow a$|+|$\overrightarrow b$|=4(1)求M(x,y)的轨迹方程C.
(2)P为曲线C上一动点,F1(-1,0),F2(1,0),求$\overrightarrow{P{F_1}}$•$\overrightarrow{P{F_2}}$的最大值和最小值;
(3)直线l与曲线C交于A,B两点,若以AB为直径的圆过原点O,试探究点O到直线l 的距离是否为定值?若是,求出该定值,若不是,说明理由.
分析 (1)根据条件便可得到$\sqrt{(x-1)^{2}+{y}^{2}}+\sqrt{(x+1)^{2}+{y}^{2}}=4$,这便说明点(x,y)到定点(-1,0),(1,0)的距离为4,从而可得到M(x,y)的轨迹为椭圆,并且椭圆方程可求出为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)可设P(x0,y0),从而可以求出$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}={{x}_{0}}^{2}-1+{{y}_{0}}^{2}$,而根据点P在椭圆上,便可消去y0得到关于x0的式子,再根据x0的范围即可得出$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$的范围,即可求出其最大、最小值;
(3)可设A(x1,y1),B(x2,y2),根据条件便得到$\overrightarrow{OA}⊥\overrightarrow{OB}$,从而可得到x1x2+y1y2=0,考虑用直线l的方程,从而讨论l的斜率:不存在斜率时,可设直线方程为x=t,联立椭圆的方程即可得出x1x2,y1y2,从而可以求出t=$±\frac{2\sqrt{21}}{7}$,这便得到O到l的距离为$\frac{2\sqrt{21}}{7}$;l存在斜率时,可设方程为y=kx+b,从而可以得到$(1+{k}^{2}){x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}=0$,而联立直线方程和椭圆方程,消去y便可得出关于x的一元二次方程,根据韦达定理即可求出x1x2,x1+x2,带入前面的式子便可以得到7m2=12(1+k2),从而可以求出点O到直线l的距离,从而判断O到l的距离是否为定值.
解答 解:(1)由$|\overrightarrow{a}|+|\overrightarrow{b}|=4$得:$\sqrt{(x-1)^{2}+{y}^{2}}+\sqrt{(x+1)^{2}+{y}^{2}}=4$;
∴点(x,y)到定点(1,0),(-1,0)的距离之和为4;
∴M(x,y)的轨迹是焦点为(-1,0),(1,0),长轴长为4的椭圆;
∴c=1,a=2,$b=\sqrt{3}$;
∴椭圆的方程,即M(x,y)的轨迹方程C为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设P(x0,y0),P点在曲线C上,∴$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$;
∴${{y}_{0}}^{2}=\frac{12-3{{x}_{0}}^{2}}{4}$;
∴$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=(-1-{x}_{0},-{y}_{0})•(1-{x}_{0},-{y}_{0})$=${{x}_{0}}^{2}-1+{{y}_{0}}^{2}$=${{x}_{0}}^{2}-1+\frac{12-3{{x}_{0}}^{2}}{4}$=$\frac{{{x}_{0}}^{2}}{4}+2$;
∵-2≤x0≤2;
∴$0≤{{x}_{0}}^{2}≤4$;
∴$2≤\frac{{{x}_{0}}^{2}}{4}+2≤3$;
∴$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$的最大值为3,最小值为2;
(3)以AB为直径的圆过原点O;
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$;
设A(x1,y1),B(x2,y2),则x1x2+y1y2=0;
①若直线l不存在斜率,设l的方程为x=t,则由:$\left\{\begin{array}{l}{x=t}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$得,${y}^{2}=\frac{12-3{t}^{2}}{4}$;
∴${x}_{1}{x}_{2}={t}^{2},{y}_{1}{y}_{2}=\frac{3{t}^{2}-12}{4}$;
∴${t}^{2}+\frac{3{t}^{2}-12}{4}=0$;
∴$t=±\frac{2\sqrt{21}}{7}$;
∴O到l的距离为$\frac{2\sqrt{21}}{7}$;
②若直线l存在斜率,设方程为y=kx+m;
∵x1x2+y1y2=0;
∴x1x2+(kx1+m)(kx2+m)=0;
$(1+{k}^{2}){x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}=0$(Ⅰ);
将y=kx+m带入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得,(3+4k2)x2+8kmx+4m2-12=0;
∴${x}_{1}+{x}_{2}=-\frac{8km}{3+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{3+4{k}^{2}}$;
带入(Ⅰ)得:7m2=12(1+k2);
∴O到直线l的距离为$\frac{|m|}{\sqrt{1+{k}^{2}}}=\frac{2\sqrt{21}}{7}$;
综上得,点O到直线l的距离为定值,定值为$\frac{2\sqrt{21}}{7}$.
点评 考查根据向量坐标求向量长度,椭圆的定义及椭圆的标准方程,椭圆上的点的横坐标的范围,以及向量垂直的充要条件,直线的点斜式方程,韦达定理,点到直线的距离公式,不要漏了直线l的斜率不存在的情况.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案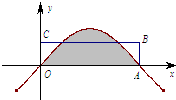 点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )
点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{4}{π}$ |
①对任意的x∈R都有f(x+2)=-f(x);
②对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),
③y=f(x+2)的图象关于y轴对称,
则下列结论中正确的是( )
| A. | f(4.5)<f(6.5)<f(7) | B. | f(7)<f(6.5)<f(4.5) | C. | f(7)<f(4.5)<f(6.5) | D. | f(4.5)<f(7)<f(6.5) |
| A. | 1.5 | B. | 3 | C. | 0.5 | D. | 3.5 |
| A. | a=a1•5-2 | B. | a=a1•2-3 | C. | a=a1•3-2 | D. | a=a1•2-5 |
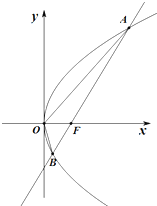 已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.
已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.