题目内容
设x＞0，y＞0且3x+2y=12，则xy的最大值是________．
6
分析：由于两个变量的和为常数，两个变量都是正数，利用基本不等式求出函数的最大值，注意验等号何时取得．
解答：∵x＞0，y＞0，
∴3x•2y≤（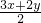
）2=62?xy≤6（当且仅当3x=2y=6时等号成立）．
故答案为6
点评：本题考查利用基本不等式求函数的最值需要注意满足的条件是：一正、二定、三相等．
分析：由于两个变量的和为常数，两个变量都是正数，利用基本不等式求出函数的最大值，注意验等号何时取得．
解答：∵x＞0，y＞0，
∴3x•2y≤（
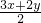）2=62?xy≤6（当且仅当3x=2y=6时等号成立）．故答案为6
点评：本题考查利用基本不等式求函数的最值需要注意满足的条件是：一正、二定、三相等．
练习册系列答案
相关题目
设过点P（x，y）的直线分别与x轴的正半轴和y轴的正半轴交于A、B两点，点Q与点P关于x轴对称，O为坐标原点，若
=2
，且
•
=-3，则P点的轨迹方程是（ ）
| BP |
| PA |
| OQ |
| AB |
A、3x2+
| ||
B、
| ||
C、
| ||
D、x2+
|
（其中i、j分别为x轴,y轴正方向上的 单位向量).有下列命题：[来源:学|科|网]
，则
的最小值为3;
，则
的最小值为
；[来源:学。科。网]
，则
的最大值为3;
，若
（其中
，若向量
且
，则动点P的轨迹是拋物线.