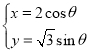题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(Ⅰ)0(Ⅱ)![]()
【解析】
(Ⅰ)对![]() 求导,利用
求导,利用![]() ,得关于
,得关于![]() 的方程解方程,即可求出
的方程解方程,即可求出![]() 的值;
的值;
(Ⅱ)当![]() 时,
时,![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,构造函数
恒成立,构造函数![]() ,利用导数判断其单调性,并对
,利用导数判断其单调性,并对![]() 进行分类讨论,即可求出
进行分类讨论,即可求出![]() 的最大值.
的最大值.
(Ⅰ)因为f![]()
所以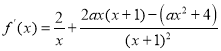
![]() ,
,
又因为曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,所以
垂直,所以![]() ,
,
所以![]() ,解得
,解得![]() .
.
(Ⅱ)由(Ⅰ)知,![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
等价于![]() 恒成立,
恒成立,
等价于![]() 恒成立.
恒成立.
设![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 恒成立,
恒成立,
所以![]() 符合题意;
符合题意;
②当![]() ,即
,即![]() 或
或![]() 时,
时,
设![]() ,
,
则![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() ,
,
所以在![]() 上存在
上存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() ,
,
所以![]() 或
或![]() 不合题意,舍去.
不合题意,舍去.
综上所述,实数![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
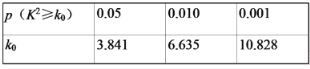
【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.