题目内容
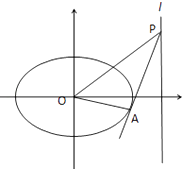
【题目】已知椭圆 ![]() +y2=1(a>1),过直线l:x=2上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为±
+y2=1(a>1),过直线l:x=2上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为± ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设O为坐标原点,求△POA面积的最小值.
【答案】解:(Ⅰ)当P点在x轴上时,P(2,0),PA: ![]() ,
, ,
,
△=0a2=2,椭圆方程为 ![]() ;
;
(Ⅱ)设切线为y=kx+m,设P(2,y0),A(x1 , y1),
则 ![]() (1+2k2)x2+4kmx+2m2﹣2=0△=0m2=2k2+1,…7
(1+2k2)x2+4kmx+2m2﹣2=0△=0m2=2k2+1,…7
且 ![]() ,y0=2k+m
,y0=2k+m
则 ![]() ,
,
PA直线为 ![]() ,A到直线PO距离
,A到直线PO距离  ,
,
则 ![]()
= 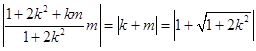 ,
,
∴(S﹣k)2=1+2k2k2+2Sk﹣S2+1=0,![]() ,此时
,此时 ![]() .
.
【解析】(Ⅰ)由P在x轴设出P点坐标及直线PA方程,将PA方程与椭圆方程联立,整理关于x的一元二次方程,△=0求得a2 , 即可求得椭圆方程;(Ⅱ)设出切线方程和点P及点A的坐标,将切线方程代入椭圆方程,求得关于x的一元二次方程,△=0,求得A和P点的坐标,求得|PA|及A到直线OP的距离,根据三角形的面积公式求得S=|k+ ![]() |,平方整理关于k的一元二次方程,△≥0,即可求得S的最小值.
|,平方整理关于k的一元二次方程,△≥0,即可求得S的最小值.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目