Question

【题目】已知，是函数的两个相邻的零点.

（1）求；

（2）若对任意，都有，求实数的取值范围．

（3）若关于的方程在上有两个不同的解，求实数的取值范围．

Answer 1

【答案】(1) ；(2) ；(3)

【解析】

（1）先化简，再根据函数的周期求出的值，从而得到的解析式；

（2）将问题转化为，根据三角函数的性质求出的最大值，即可求出实数的取值范围；（3）通过方程的解与函数图象之间的交点关系，可将题意转化为函数 的图象与直线有两个交点，即可由图象求出实数的取值范围．

（1）

。

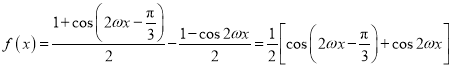
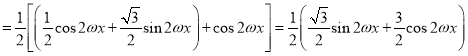
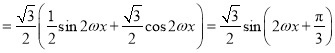由题意可知，的最小正周期，

∴，又∵，∴，

∴

（2）由得，，∴，

∵，∴，∴。

∴，即，

∴，所以

（3）原方程可化为

即，

由，得

时，，的最大值为2，

∴要使方程在上有两个不同的解，即函数 的图象与直线有两个交点，由图象可知，即，

所以