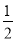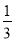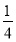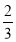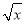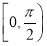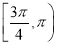题目内容
设f(x)=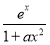 ,其中a为正实数.
,其中a为正实数.
①当a=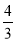 时,求f(x)的极值点;②若f(x)为R上的单调函数,求a的取值范围.
时,求f(x)的极值点;②若f(x)为R上的单调函数,求a的取值范围.
①x= 是极大值点,x=
是极大值点,x= 是极小值点②(0,1]
是极小值点②(0,1]
【解析】f′(x)=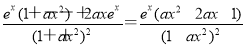
①当a=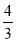 时,f′(x)=
时,f′(x)= .由f′(x)=0得x=
.由f′(x)=0得x=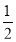 或x=
或x=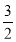 .
.
当x<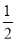 时,f′(x)>0;当
时,f′(x)>0;当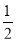 <x<
<x< 时,f′(x)<0;当x>
时,f′(x)<0;当x>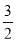 时,f′(x)>0.
时,f′(x)>0.
∴f(x)在 上是增函数,
上是增函数, 上是减函数,
上是减函数,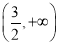 上是增函数.
上是增函数.
∴x= 是极大值点,x=
是极大值点,x= 是极小值点.
是极小值点.
②若f(x)为R上的单调函数,则f′(x)在R上不变号.由于a>0,又ex>0,(1+ax2)2>0.∴ax2-2ax+1≥0在R上恒成立.即Δ=4a2-4a≤0.
∴0<a≤1.所以a的范围为(0,1].

练习册系列答案
相关题目