题目内容

10．设lg2=a，则log225=（　　）
A．$\frac{1-a}{a}$B．$\frac{a}{1-a}$C．$\frac{2（1-a）}{a}$D．$\frac{2a}{1-a}$

分析 根据对数的运算性质和换底公式即可求出．

解答 解：lg2=a，
则log225=$\frac{lg25}{lg2}$=$\frac{lg\frac{100}{4}}{lg2}$=$\frac{lg100-lg4}{lg2}$=$\frac{2-2a}{a}$，
故选：C．

点评 本题考查了对数的运算性质和换底公式，属于基础题．

练习册系列答案
相关题目
20．不等式|x+2|＞2的解集为（　　）
A．∅B．（0，+∞）C．（-∞，-4）∪（0，+∞）D．R
1．已知函数f（x）=x-m+3（m∈N）为偶函数且f（3）＜f（5），求f（x）的解析式．
18．设△ABC的角A，B，C的对边分别为a，b，c，已知A，B，C成等差数列．
（1）若a，b，c成等比数列，求A，B，C；
（2）若$\overrightarrow{BA}•\overrightarrow{BC}=12$，b=2$\sqrt{7}$，求a，c．
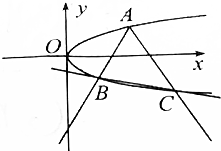5．如图，过抛物线y2=x上一点A（4，2）作倾斜角互补的两条直线AB，AC，交抛物线于B，C两点，求证：直线BC的斜率是定值．
15．若关于x的不等式$\frac{x-a}{x+1}$＞0的解集为（-∞，-1）∪（$\frac{1}{2}$，+∞），则实数a=$\frac{1}{2}$．
2．下列式子中：①lg（3+2$\sqrt{2}$）-lg（3-2$\sqrt{2}$）=0；
②lg（10+$\sqrt{99}$）•lg（10-$\sqrt{99}$）=0；
③log${\;}_{\sqrt{n+1}-\sqrt{n}}$（$\sqrt{n+1}$+$\sqrt{n}$）=-1（n∈N*）
④$\frac{lga}{lgb}$=lg（a-b）．
其中正确的有③． （填序号）
19．已知lga、lgb是方程x2-4x+1=0的两个根，则lg2$\frac{a}{b}$的值是（　　）
A．14B．15C．13D．12
10．下列说法正确的有（　　）
①方向相同的向量叫相等向量；
②零向量的长度为0；
③共线向量是在同一条直线上的向量；
④零向量是没有方向的向量；
⑤共线向量不一定相等；
⑥平行向量方向相同．
A．2个B．3个C．4个D．5个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网