题目内容
15.判断下列函数的单调性:(1)f(x)=5x+1;
(2)f(x)=-4x+3.
分析 利用判断函数单调性的定义:设任意的x1,x2,且x1<x2,判断f(x1)-f(x2)的正负即可.
解答 解:(1)设任意的x1,x2,且x1<x2
∴f(x1)-f(x2)=5x1+1-(5x2+1)
=5(x1-x2)<0,
∴f(x1)<f(x2),
∴函数f(x)=5x+1在R上单调递增;
(2)设任意的x1,x2,且x1<x2,
∴f(x1)-f(x2)=-4x1+3-(-4x2+3)
=4(x2-x1)>0,
∴函数f(x)=-4x+3在R上单调递减.
点评 考察了利用定义法判断函数的单调性,需先求出定义域,利用定义法证明.属于常规提醒,应熟练掌握.

练习册系列答案
相关题目
20.不等式|x+2|>2的解集为( )
| A. | ∅ | B. | (0,+∞) | C. | (-∞,-4)∪(0,+∞) | D. | R |
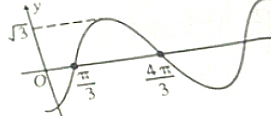 设函数f(x)=Asin(ωx+φ)x∈R,ω>0,|φ|<π),其导函数y=f′(x)的部分图象如图所示,
设函数f(x)=Asin(ωx+φ)x∈R,ω>0,|φ|<π),其导函数y=f′(x)的部分图象如图所示,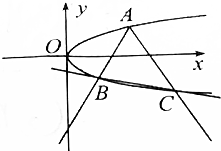 如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.
如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.