题目内容
12.已知四组函数:①$y=\sqrt{x^2}-1$与$y=\root{3}{x^3}-1$;②f(x)=x0与$g(x)=\frac{1}{x^0}$;③$y=\frac{x^2}{|x|}$与$y=\left\{{\begin{array}{l}{t,t>0}\\{-t,t<0}\end{array}}\right.$;④f(x)=2x,D={0,1,2,3}与$g(x)=\frac{1}{6}{x^3}+\frac{5}{6}x+1,D=\left\{{0,1,2,3}\right\}$.表示同一函数的是②③.(写出所有符合要求的函数组的序号)分析 根据定义域和解析式一致的两个函数表示同一函数,逐一分析四组函数的定义域和解析式,可得结论.
解答 解:①中,$y=\sqrt{x^2}-1$=|x|-1,$y=\root{3}{x^3}-1$=x-1,解析式不一致,不是同一函数;
②中,f(x)=x0=1(x≠0),$g(x)=\frac{1}{x^0}$=1(x≠0),定义域,解析式均一致,是同一函数;
③中,$y=\frac{x^2}{|x|}$=|x|,(x≠0),$y=\left\{{\begin{array}{l}{t,t>0}\\{-t,t<0}\end{array}}\right.$,定义域,解析式均一致,是同一函数;
④中,f(x)=2x,D={0,1,2,3}与$g(x)=\frac{1}{6}{x^3}+\frac{5}{6}x+1,D=\left\{{0,1,2,3}\right\}$,解析式不一致,不是同一函数.
故表示同一函数的是:②③,
故答案为:②③
点评 本题考查的知识点是判断两个函数是否为同一函数,正确理解同一函数的定义,是解答的关键.

练习册系列答案
相关题目
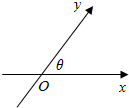 如图,数轴x,y的交点为O,夹角为θ,与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1},\overrightarrow{e_2}$.由平面向量基本定理,对于平面内的任一向量$\overrightarrow{OP}$,存在唯一的有序实数对(x,y),使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,我们把(x,y)叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标).
如图,数轴x,y的交点为O,夹角为θ,与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1},\overrightarrow{e_2}$.由平面向量基本定理,对于平面内的任一向量$\overrightarrow{OP}$,存在唯一的有序实数对(x,y),使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,我们把(x,y)叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标).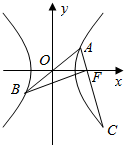 如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$.
如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$.