题目内容
20.已知集合$A=\left\{{x\left|{\frac{{{x^2}-x-6}}{x+1}≤0}\right.}\right\}$,集合B={x||x+2a|≤a+1,a∈R}.(1)求集合A与集合B;
(2)若A∩B=B,求实数a的取值范围.
分析 (1)求出A中不等式的解集确定出A,表示出B中不等式的解集确定出B即可;
(2)由A与B的交集为B,得到B为A的子集,确定出a的范围即可.
解答 解:(1)由A中方程变形得:(x-3)(x+2)(x+1)≤0,
解得:x≤-2或-1<x≤3,即A=(-∞,-2]∪(-1,3],
当a+1<0时,即a<-1时,B=∅;
当a+1≥0时,即a≥-1时,B=[-3a-1,-a+1];
(2)∵A∩B=B,
∴B⊆A,
当a<-1时,B=∅满足题意;
当a≥-1时,B=[-3a-1,-a+1],
此时有:-a+1≤-2或$\left\{\begin{array}{l}-1<-3a-1\\-a+1≤3\end{array}\right.$,
解得,a≥3或-1≤a<0,
综上所述,a∈(-∞,0)∪[3,+∞).
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
11.化简$\sqrt{{{(π-4)}^2}}+\root{3}{{{{(π-5)}^3}}}$的结果是( )
| A. | 2π-9 | B. | 9-2π | C. | -1 | D. | 1 |
9.下列命题中真命题是( )
| A. | 若$\overrightarrow{a}$与$\overrightarrow{b}$互为负向量,则$\overrightarrow{a}$+$\overrightarrow{b}$=0 | B. | 若 $\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若k为实数且k$\overrightarrow{a}$=$\overrightarrow{0}$,则k=0或$\overrightarrow{a}$=$\overrightarrow{0}$ | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| |
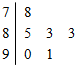 为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则该同学数学成绩的中位数为84.
为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则该同学数学成绩的中位数为84.