题目内容
等比数列{an}中，a2=4，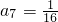
，则a3a6+a4a5的值是
- A.1
- B.2
- C.
- D.
C
分析：由等比数列的定义和性质可得 a3a6=a4a5=a2•a7，由此求得a3a6+a4a5的值．
解答：∵等比数列{an}中，a2=4，，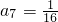
∴a3a6=a4a5=a2•a7=4×
=，
故a3a6+a4a5 =+=，
故选C．
点评：本题主要考查等比数列的定义和性质，属于基础题．
分析：由等比数列的定义和性质可得 a3a6=a4a5=a2•a7，由此求得a3a6+a4a5的值．
解答：∵等比数列{an}中，a2=4，
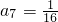，∴a3a6=a4a5=a2•a7=4×
=，故a3a6+a4a5 =
+=，故选C．
点评：本题主要考查等比数列的定义和性质，属于基础题．
练习册系列答案
相关题目