题目内容
如图,在四棱椎P-ABCD中,底面ABCD是边长为 的正方形,且PD=
的正方形,且PD= ,PA=PC=
,PA=PC=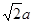 .
.

(1)求证:直线PD⊥面ABCD;
(2)求二面角A-PB-D的大小.
 的正方形,且PD=
的正方形,且PD= ,PA=PC=
,PA=PC=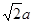 .
.
(1)求证:直线PD⊥面ABCD;
(2)求二面角A-PB-D的大小.
(1)见解析;(2)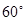 .
.
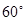 .
.(1)本小题可通过证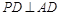 ,和
,和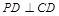 来达到证明直线PD⊥面ABCD的目的。
来达到证明直线PD⊥面ABCD的目的。
(2)解决本小题的关键是作出二面角的平面角,取AP中点H,过H作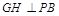 于G,连结DG。则
于G,连结DG。则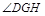 为所求二面角平面角,然后解三角形求角即可。
为所求二面角平面角,然后解三角形求角即可。
解:(1) 在
在 中,
中,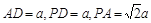 ,
,
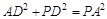
即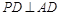 ,同理
,同理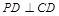 又AD、CD
又AD、CD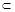 平面ABCD,
平面ABCD,
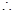 直线PD
直线PD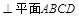
(2)解法一:
如图,连结AC和BD,设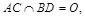
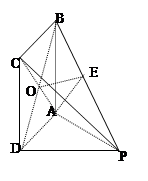
由(1)知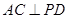 ,又
,又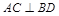 ,且
,且
PD、BD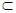 平面PBD,
平面PBD,
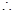 直线AC
直线AC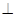 平面PBD,
平面PBD,
过点O作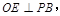 E为垂足,连结AE,由三垂线定理知
E为垂足,连结AE,由三垂线定理知
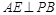 ,
, 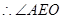 为二面角A-PB-D的平面角
为二面角A-PB-D的平面角
 AB
AB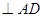 ,所以
,所以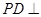 面ABCD,故AB
面ABCD,故AB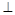 PD,
PD,
从而AB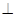 面PAD,故AB
面PAD,故AB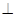 PA,
PA,
 在
在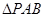 中,
中,
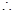 在
在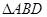 中,
中,
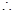
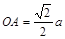
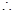 在
在 中,
中,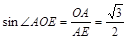
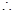 二面角A-PB-D的平面角为
二面角A-PB-D的平面角为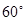 .
.
解法二:取AP中点H,过H作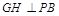 于G,连结DG
于G,连结DG
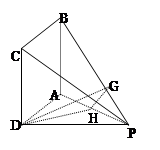
则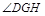 为所求二面角平面角,
为所求二面角平面角, 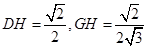
解法三:利用空间向量
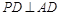 ,和
,和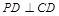 来达到证明直线PD⊥面ABCD的目的。
来达到证明直线PD⊥面ABCD的目的。(2)解决本小题的关键是作出二面角的平面角,取AP中点H,过H作
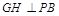 于G,连结DG。则
于G,连结DG。则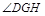 为所求二面角平面角,然后解三角形求角即可。
为所求二面角平面角,然后解三角形求角即可。解:(1)
 在
在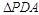 中,
中,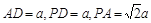 ,
,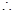
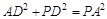
即
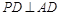 ,同理
,同理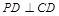 又AD、CD
又AD、CD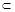 平面ABCD,
平面ABCD,
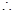 直线PD
直线PD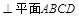
(2)解法一:
如图,连结AC和BD,设
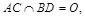
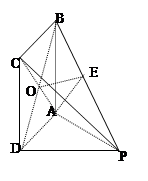
由(1)知
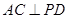 ,又
,又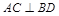 ,且
,且PD、BD
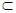 平面PBD,
平面PBD,
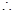 直线AC
直线AC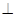 平面PBD,
平面PBD,过点O作
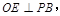 E为垂足,连结AE,由三垂线定理知
E为垂足,连结AE,由三垂线定理知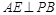 ,
, 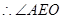 为二面角A-PB-D的平面角
为二面角A-PB-D的平面角 AB
AB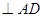 ,所以
,所以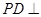 面ABCD,故AB
面ABCD,故AB PD,
PD,从而AB
 面PAD,故AB
面PAD,故AB PA,
PA, 在
在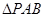 中,
中,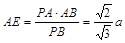
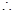 在
在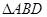 中,
中,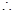
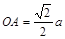
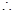 在
在 中,
中,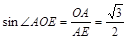
 二面角A-PB-D的平面角为
二面角A-PB-D的平面角为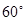 .
.解法二:取AP中点H,过H作
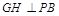 于G,连结DG
于G,连结DG
则
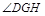 为所求二面角平面角,
为所求二面角平面角, 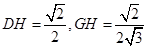
解法三:利用空间向量

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
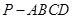 中,底面
中,底面 是矩形,
是矩形,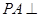 平面
平面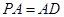 ,
,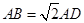 ,
,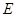 是线段
是线段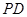 上的点,
上的点,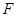 是线段
是线段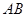 上的点,且
上的点,且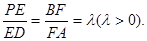

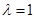 时,证明
时,证明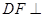 平面
平面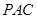 ;
;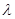 ,使异面直线
,使异面直线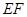 与
与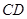 所成的角为
所成的角为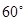 ?若存在,试求出
?若存在,试求出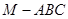 中,
中,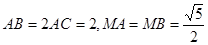 ,
,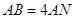 ,
,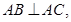 平面
平面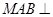 平面
平面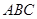 ,
,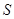 为
为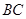 的中点.
的中点.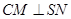 ;
;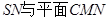 所成角的大小.
所成角的大小.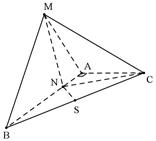
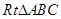 中,
中,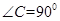 ,D,E分别为AC,AB的中点,点F为线段CD上的一点,将
,D,E分别为AC,AB的中点,点F为线段CD上的一点,将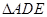 沿DE折起到
沿DE折起到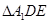 的位置,使
的位置,使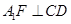 ,如图2.
,如图2.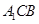
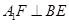
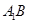 上是否存在点Q,使
上是否存在点Q,使 ?说明理由。
?说明理由。
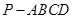 中,底面
中,底面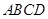 是菱形,
是菱形,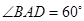 ,
,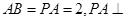 底面
底面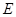 是
是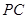 的中点,
的中点,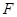 是
是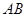 中点。
中点。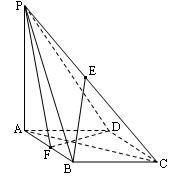
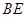 ∥平面
∥平面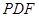 ;
;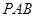 ;
;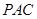 所成的角。
所成的角。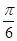 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD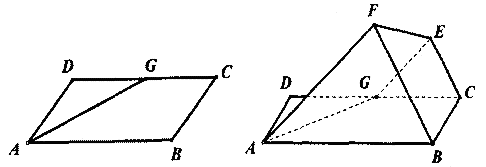
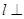 平面
平面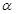 ,直线
,直线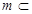 平面
平面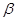 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )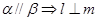 ②
②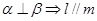 ;③
;③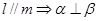 ;④
;④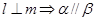
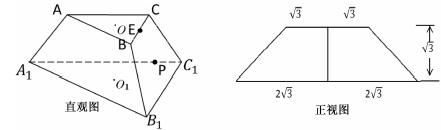
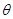 角的直线一定有无穷多条。
角的直线一定有无穷多条。