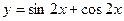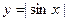题目内容
(Ⅰ)当
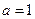 时,证明函数
时,证明函数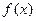 只有一个零点;
只有一个零点;(Ⅱ)若函数
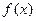 在区间
在区间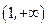 上是减函数,求实数
上是减函数,求实数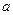 的取值范围
的取值范围(Ⅱ)

(Ⅰ)当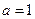 时,
时, ,其定义域是
,其定义域是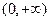
∴ …………2分
…………2分
令 ,即
,即 ,解得
,解得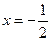 或
或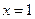 .
.
 ,∴
,∴  舍去.
舍去.
当 时,
时, ;当
;当 时,
时, .
.
∴ 函数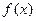 在区间
在区间 上单调递增,在区间
上单调递增,在区间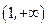 上单调递减
上单调递减
∴ 当x =1时,函数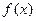 取得最大值,其值为
取得最大值,其值为 .
.
当 时,
时,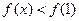 ,即
,即 .
.
∴ 函数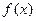 只有一个零点. ……………………6分
只有一个零点. ……………………6分
(Ⅱ)显然函数 的定义域为
的定义域为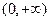
∴ ………7分
………7分
①当 时,
时,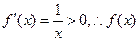 在区间
在区间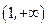 上为增函数,不合题意……8分
上为增函数,不合题意……8分
② 当 时,
时,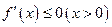 等价于
等价于 ,即
,即
此时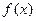 的单调递减区间为
的单调递减区间为 .
.
依题意,得 解之得
解之得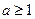 . ………10分
. ………10分
③ 当 时,
时,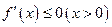 等价于
等价于 ,即
,即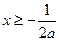
此时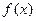 的单调递减区间为
的单调递减区间为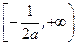 ,
,
∴ 得
得
综上,实数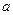 的取值范围是
的取值范围是 …………12分
…………12分
法二:
①当 时,
时,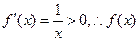 在区间
在区间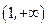 上为增函数,不合题意……8分
上为增函数,不合题意……8分
②当 时,要使函数
时,要使函数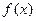 在区间
在区间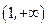 上是减函数,只需
上是减函数,只需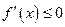 在区间
在区间
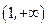 上恒成立,
上恒成立,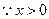
 只要
只要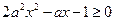 恒成立,
恒成立,
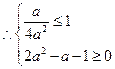 解得
解得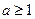 或
或
综上,实数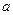 的取值范围是
的取值范围是 …………12分
…………12分
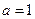 时,
时, ,其定义域是
,其定义域是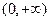
∴
 …………2分
…………2分 令
 ,即
,即 ,解得
,解得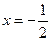 或
或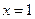 .
. ,∴
,∴  舍去.
舍去. 当
 时,
时, ;当
;当 时,
时, .
.∴ 函数
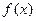 在区间
在区间 上单调递增,在区间
上单调递增,在区间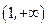 上单调递减
上单调递减∴ 当x =1时,函数
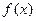 取得最大值,其值为
取得最大值,其值为 .
.当
 时,
时,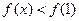 ,即
,即 .
.∴ 函数
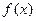 只有一个零点. ……………………6分
只有一个零点. ……………………6分(Ⅱ)显然函数
 的定义域为
的定义域为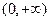
∴
 ………7分
………7分①当
 时,
时,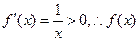 在区间
在区间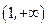 上为增函数,不合题意……8分
上为增函数,不合题意……8分② 当
 时,
时,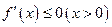 等价于
等价于 ,即
,即
此时
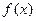 的单调递减区间为
的单调递减区间为 .
.依题意,得
 解之得
解之得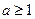 . ………10分
. ………10分 ③ 当
 时,
时,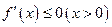 等价于
等价于 ,即
,即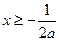
此时
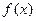 的单调递减区间为
的单调递减区间为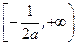 ,
,∴
 得
得
综上,实数
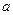 的取值范围是
的取值范围是 …………12分
…………12分法二:
①当
 时,
时,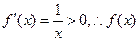 在区间
在区间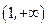 上为增函数,不合题意……8分
上为增函数,不合题意……8分②当
 时,要使函数
时,要使函数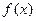 在区间
在区间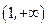 上是减函数,只需
上是减函数,只需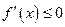 在区间
在区间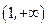 上恒成立,
上恒成立,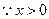
 只要
只要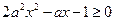 恒成立,
恒成立,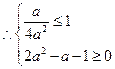 解得
解得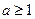 或
或
综上,实数
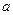 的取值范围是
的取值范围是 …………12分
…………12分
练习册系列答案
相关题目
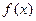 满足
满足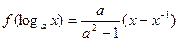 ,其中
,其中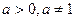 ,
, 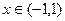 时,
时,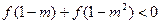 ,求实数
,求实数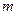 的集合;
的集合; 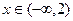 时,
时,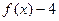 的值恒为负数,求
的值恒为负数,求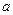 的取值范围.
的取值范围.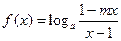
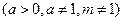
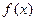 在
在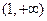 上的单调性,并给出证明;
上的单调性,并给出证明;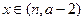 Í
Í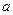 与
与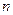
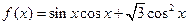
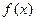 的最小正周期;
的最小正周期;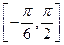 上的最大值和最小值
上的最大值和最小值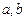 的值
的值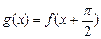 ,且
,且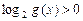 ,求
,求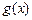 的单调区间
的单调区间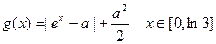 ,求函数
,求函数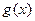 的最小值
的最小值 )=0,当x>-
)=0,当x>-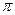 为最小正周期的偶函数,且在
为最小正周期的偶函数,且在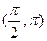 上为减函数的是 ( )
上为减函数的是 ( )