题目内容
3.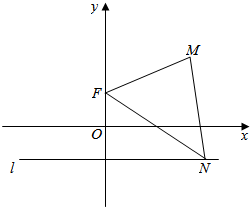 如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.
如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.(1)求动点M的轨迹C的方程;
(2)设Q是l上的任意一点,过Q作轨迹C的切线,切点为A、B.
①求证:A、Q、B三点的横坐标成等差数列;
②若Q(-4,-p),AB=20,求P的值.
分析 (1)设点M(x,y),则 N(x,-p),又 F(0,p),分别求得向量NM,NF,FM,FN的坐标,再由向量的数量积的坐标表示,化简可得4py=x2,即为所求的动点M的轨迹方程;
(2)①设A(x1,$\frac{{{x}_{1}}^{2}}{4p}$),B(x2,$\frac{{{x}_{2}}^{2}}{4p}$),Q(m,-p),设切线为y+p=k(x-m),联立抛物线方程x2=4py,运用判别式为0和韦达定理,及等差数列的性质,计算即可得到;
②由两点的距离公式,结合①的结论,即可解得p=1.
解答 解:(1)设点M(x,y),则 N(x,-p),
又 F(0,p),
则 $\overrightarrow{NM}$=(0,p+y),$\overrightarrow{NF}$=(-x,2p),$\overrightarrow{FM}$=(x,y-p),$\overrightarrow{FN}$=(x,-2p),
由$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$,可得2p(p+y)=x2-2p(y-p),
化简可得4py=x2,
动点M的轨迹C的方程为x2=4py;
(2)①证明:设A(x1,$\frac{{{x}_{1}}^{2}}{4p}$),B(x2,$\frac{{{x}_{2}}^{2}}{4p}$),Q(m,-p),
设切线为y+p=k(x-m),
联立抛物线方程x2=4py,
可得x2-4pkx+4p(km+p)=0,
由判别式为0,即16p2k2-16p(km+p)=0,
即pk2-km-p=0,
即有k1+k2=$\frac{m}{p}$,k1k2=-1,
可得切点的横坐标为x1=2pk1,
x2=2pk2,
可得x1+x2=2p(k1+k2)=2m,
故A、Q、B三点的横坐标成等差数列;
②由①可得x1+x2=2p(k1+k2)=2m=-8,
x1x2=4p2•(k1k2)=-4p2,
则|AB|=$\sqrt{({x}_{1}-{x}_{2})^{2}+(\frac{{{x}_{1}}^{2}}{4p}-\frac{{{x}_{2}}^{2}}{4p})^{2}}$
=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$•$\sqrt{1+\frac{({x}_{1}+{x}_{2})^{2}}{16{p}^{2}}}$
=$\sqrt{64+16{p}^{2}}$•$\sqrt{1+\frac{64}{16{p}^{2}}}$=20,
解得p=1.
点评 本题考查轨迹方程的求法,考查向量的数量积的坐标表示,同时考查直线和抛物线方程联立,运用韦达定理,以及直线和抛物线相切的条件,两点间的距离公式的运用,考查运算能力,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案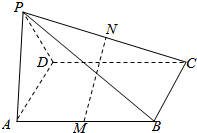 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC. 在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,
在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,