题目内容
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ).
).
(Ⅰ)若![]() 是函数
是函数![]() 的一个极值点,求
的一个极值点,求![]() 的值;
的值;
(Ⅱ)求证:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅲ)若对任意的![]() (1,2),总存在
(1,2),总存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取范围.
的取范围.
【答案】(Ⅰ)![]() .
.
(Ⅱ)略
(Ⅲ)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
本试题主要是考查了导数在研究函数中的运用.以及不等是的求解,和函数单调性的判定的综合运用.
(1)因为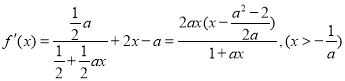
由已知,得![]() 即
即![]() , 得到a的值,
, 得到a的值,
(2)当![]() 时,
时,![]()
![]()
![]() 当
当![]() 时,
时,![]() .又
.又![]() ,
,![]() 故
故![]() 在
在![]() 上是增函数
上是增函数
(3)当![]() 时,由(Ⅱ)知,
时,由(Ⅱ)知,![]() 在
在![]() 上的最大值为
上的最大值为![]()
于是问题等价于:对任意的![]() ,不等式
,不等式![]() 恒成立.
恒成立.
利用构造函数得到结论.
解: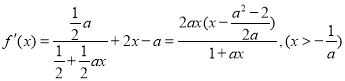 ……………1分
……………1分
(Ⅰ)由已知,得![]() 即
即![]() ,
,![]() ……3分
……3分
经检验,![]() 满足条件.……………………………………4分
满足条件.……………………………………4分
(Ⅱ)当![]() 时,
时,![]()
![]() …………5分
…………5分
![]() 当
当![]() 时,
时,![]() .又
.又![]() ,
,![]() 故
故![]() 在
在![]() 上是增函数
上是增函数
(Ⅲ)当![]() 时,由(Ⅱ)知,
时,由(Ⅱ)知,![]() 在
在![]() 上的最大值为
上的最大值为![]()
于是问题等价于:对任意的![]() ,不等式
,不等式![]() 恒成立.
恒成立.
记![]()
则![]() …………………………9分
…………………………9分
当![]() 时,有
时,有![]() ,且
,且![]() 在区间(1,2)上递减,且
在区间(1,2)上递减,且![]() ,则
,则![]() 不可能使
不可能使![]() 恒成立,故必有
恒成立,故必有![]() …………11分
…………11分
当![]() ,且
,且![]()
若![]() ,可知
,可知![]() 在区间
在区间![]() 上递减,在此区间
上递减,在此区间![]() 上有
上有![]() ,与
,与![]() 恒成立矛盾,故
恒成立矛盾,故![]() ,这时
,这时![]() ,即
,即![]() 在(1,2)上递增,恒有
在(1,2)上递增,恒有![]() 满足题设要求.
满足题设要求.
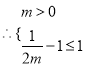 ,即
,即![]() ,所以,实数
,所以,实数![]() 的取值范围为
的取值范围为![]() .……………………14分
.……………………14分

【题目】近几年来我国电子商务行业发展迅猛,2016年元旦期间,某购物平台的销售业绩高达918亿人民币,与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)完成商品和服务评价的![]() 列联表,并说明是否可以在犯错误的概率不超过
列联表,并说明是否可以在犯错误的概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品和服务全好评的次数为随机变量![]() .
.
①求对商品和服务全好评的次数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
参考数据及公式如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(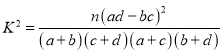 ,其中
,其中![]() )
)