题目内容

（2012•包头一模）选修4-5；不等式选讲．
设不等式|2x-1|＜1的解集是M，a，b∈M．
（I）试比较ab+1与a+b的大小；
（II）设max表示数集A的最大数．h=max{
2
a
，
a2+b2
ab
，
2
b
}，求证：h≥2．
分析：（I）解绝对值不等式求出M=（ 0，1），可得 0＜a＜1，0＜b＜1，再由（ab+1）-（a+b）=（a-1）（b-1）＞0可得ab+1与a+b的大小．
（II）由题意可得 h≥
2
a
，h≥
a2+b2
ab
，h≥
2
b
，可得 h3≥
2
a
•
a2+b2
ab
•
2
b
=
(  a2+b 2)
ab
≥8，从而证得 h≥2．
解答：解：（I）由不等式|2x-1|＜1 可得-1＜2x-1＜1，解得 0＜x＜1，从而求得 M=（ 0，1）．
由 a，b∈M，可得 0＜a＜1，0＜b＜1．
∴（ab+1）-（a+b）=（a-1）（b-1）＞0，
∴（ab+1）＞（a+b）．
（II）设max表示数集A的最大数，∵h=max{
2
a
，
a2+b2
ab
，
2
b
}，
∴h≥
2
a
，h≥
a2+b2
ab
，h≥
2
b
，
∴h3≥
2
a
•
a2+b2
ab
•
2
b
=
(  a2+b 2)
ab
≥8，故 h≥2．
点评：本题主要考查绝对值不等式的解法，不等式的性质以及基本不等式的应用，属于中档题．
练习册系列答案
相关题目
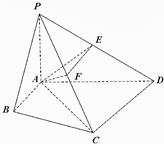（2012•包头一模）在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2，AB=1．
（Ⅰ）求四棱锥P-ABCD的体积V；
（Ⅱ）若F为PC的中点，求证：平面PAC⊥平面AEF．
（2012•包头一模）下列命题错误的是（　　）
（2012•包头一模）已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）与抛物线y2=8x有 一个公共的焦点F，且两曲线的一个交点为P，若|PF|=5，则双曲线方程为
x2-
y2
3
=1
x2-
y2
3
=1
．
（2012•包头一模）函数f（x）=sin（ωx+?）（其中|?|＜
π
2
）的图象如图所示，为了得到y=sinωx的图象，只需把y=f（x）的图象上所有点（　　）
（2012•包头一模）在平面直角坐标系xoy中，曲线C1的参数方程为 
x=acosφ
y=bsinφ
（a＞b＞0，?为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2是圆心在极轴上，且经过极点的圆．已知曲线C1上的点M（1，
3
2
）对应的参数φ=
π
3
，曲线C2过点D（1，
π
3
）．
（Ⅰ）求曲线C1，C2的直角坐标方程；
（Ⅱ）若点A（ρ 1，θ），B（ρ 2，θ+
π
2
） 在曲线C1上，求
1
ρ
2
1
+
1
ρ
2
2
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网