题目内容
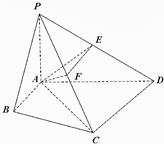 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证:平面PAC⊥平面AEF.
分析:(Ⅰ)在Rt△ABC中,AB=1,∠BAC=60°,故BC=
,AC=2,由此能求出四棱锥P-ABCD的体积V.
(Ⅱ)由PA⊥平面ABCD,知PA⊥CD,由此能证明平面PAC⊥平面AEF.
| 3 |
(Ⅱ)由PA⊥平面ABCD,知PA⊥CD,由此能证明平面PAC⊥平面AEF.
解答:解:(Ⅰ)在Rt△ABC中,AB=1,∠BAC=60°,
∴BC=
,AC=2…(2分)
在Rt△ACD中,AC=2,∠CAD=60°,CD=2
…(4分)
∵S四边形ABCD=
AB•BC+
AC•CD=
×1×
+
×2×2
=
,
则V=
×
×2=
…(6分)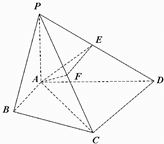
证:(Ⅱ)∵PA⊥平面ABCD,
∴PA⊥CD…(7分)
又AC⊥CD,PA∩AC=A
∴CD⊥平面PAC,…(8分)
∵E、F分别是PD、PC的中点,∴EF∥CD
∴EF⊥平面PAC…(10分),
∵EF?平面AEF,
∴平面PAC⊥平面AEF…(12分)
∴BC=
| 3 |
在Rt△ACD中,AC=2,∠CAD=60°,CD=2
| 3 |
∵S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
则V=
| 1 |
| 3 |
| 5 |
| 2 |
| 3 |
| 5 |
| 3 |
| 3 |

证:(Ⅱ)∵PA⊥平面ABCD,
∴PA⊥CD…(7分)
又AC⊥CD,PA∩AC=A
∴CD⊥平面PAC,…(8分)
∵E、F分别是PD、PC的中点,∴EF∥CD
∴EF⊥平面PAC…(10分),
∵EF?平面AEF,
∴平面PAC⊥平面AEF…(12分)
点评:本题考查棱锥的体积的求法,考查平面与平面垂直的证明,解题时要认真审题,注意合理地化立体问题为平面问题.

练习册系列答案
相关题目
 (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中