题目内容
(2012•包头一模)在平面直角坐标系xoy中,曲线C1的参数方程为
(a>b>0,?为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,
)对应的参数φ=
,曲线C2过点D(1,
).
(Ⅰ)求曲线C1,C2的直角坐标方程;
(Ⅱ)若点A(ρ 1,θ),B(ρ 2,θ+
) 在曲线C1上,求
+
的值.
|
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
(Ⅰ)求曲线C1,C2的直角坐标方程;
(Ⅱ)若点A(ρ 1,θ),B(ρ 2,θ+
| π |
| 2 |
| 1 | ||
|
| 1 | ||
|
分析:(I)将M(1,
)及对应的参数?=
,代入曲线C1的参数方程,求出a、b的值,可得曲线C1的方程.把点D的
极坐标化为直角坐标代入圆C2的方程为(x-R)2+y2=R2 ,求得R=1,即可得到曲线C2的方程.
(II)把A、B两点的极坐标化为直角坐标,代入曲线C1的方程可得
+
sin2θ=1,
+
cos2θ=1,从而求得
+
的值.
| ||
| 2 |
| π |
| 3 |
极坐标化为直角坐标代入圆C2的方程为(x-R)2+y2=R2 ,求得R=1,即可得到曲线C2的方程.
(II)把A、B两点的极坐标化为直角坐标,代入曲线C1的方程可得
| ||
| 4 |
| ρ | 2 1 |
| ||
| 4 |
| ρ | 2 2 |
| 1 | ||
|
| 1 | ||
|
解答:解:(I)将M(1,
)及对应的参数?=
,代入
,得
,即
,
所以曲线C1的方程为
+y2=1.
设圆C2的半径为R,由题意圆C2的方程为(x-R)2+y2=R2 .
由D的极坐标 (1,
),得D(
,
),代入(x-R)2+y2=R2,解得R=1,
所以曲线C2的方程为(x-1)2+y2 =1.
(II)因为点A(ρ1,θ),B(ρ2,θ+
)在曲线C1上,又点A的直角坐标为(ρ1cosθ,ρ1sinθ),
点B的横坐标为ρ2 cos(θ+
)=-ρ2sinθ,点B的纵坐标为ρ2sin(θ+
)=ρ2cosθ,
所以
+
sin2θ=1,
+
cos2θ=1,
所以
+
=(
+sin2θ)+(
+cos2θ)=
.(10分)
| ||
| 2 |
| π |
| 3 |
|
|
|
所以曲线C1的方程为
| x2 |
| 4 |
设圆C2的半径为R,由题意圆C2的方程为(x-R)2+y2=R2 .
由D的极坐标 (1,
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
所以曲线C2的方程为(x-1)2+y2 =1.
(II)因为点A(ρ1,θ),B(ρ2,θ+
| π |
| 2 |
点B的横坐标为ρ2 cos(θ+
| π |
| 2 |
| π |
| 2 |
所以
| ||
| 4 |
| ρ | 2 1 |
| ||
| 4 |
| ρ | 2 2 |
所以
| 1 | ||
|
| 1 | ||
|
| cos2θ |
| 4 |
| sin2θ |
| 4 |
| 5 |
| 4 |
点评:本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
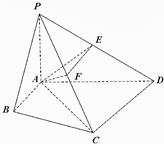 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1. (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中