题目内容
(2012•包头一模)已知双曲线
-
=1(a>0,b>0)与抛物线y2=8x有 一个公共的焦点F,且两曲线的一个交点为P,若|PF|=5,则双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
x2-
=1
| y2 |
| 3 |
x2-
=1
.| y2 |
| 3 |
分析:根据双曲线
-
=1(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,可得双曲线的右焦点坐标为F(2,0),双曲线的左焦点坐标为F′(-2,0),利用|PF|=5,可求P的坐标,从而可求双曲线方程.
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:抛物线y2=8x的焦点坐标为(2,0),准线方程为直线x=-2
∵双曲线
-
=1(a>0,b>0)与抛物线y2=8x有一个公共的焦点F
∴双曲线的右焦点坐标为F(2,0),
∴双曲线的左焦点坐标为F′(-2,0)
∵|PF|=5
∴点P的横坐标为3
代入抛物线y2=8x,y=±2
不妨设P(3,2
)
∴根据双曲线的定义,|PF'|-|PF|=2a 得出
-
=2a
∴a=1,
∵c=2
∴b=
∴双曲线方程为x2-
=1
故答案为:x2-
=1
∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴双曲线的右焦点坐标为F(2,0),
∴双曲线的左焦点坐标为F′(-2,0)
∵|PF|=5
∴点P的横坐标为3
代入抛物线y2=8x,y=±2
| 6 |
不妨设P(3,2
| 6 |
∴根据双曲线的定义,|PF'|-|PF|=2a 得出
| 25+24 |
| 1+24 |
∴a=1,
∵c=2
∴b=
| 3 |
∴双曲线方程为x2-
| y2 |
| 3 |
故答案为:x2-
| y2 |
| 3 |
点评:本题重点考查双曲线的标准方程,考查抛物线的定义,有一定的综合性.

练习册系列答案
相关题目
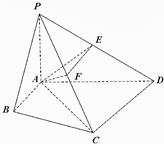 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1. (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中