题目内容
方程x3﹣6x2+9x﹣4=0的实根的个数为（ ）
| A．0 | B．1 | C．2 | D．3 |
C
解析试题分析：令
，则
，
令
得
或
。解
得，
或
；解
得，
。所以函数
在
和
上单调递增，在
上单调递减。所以当时，函数取得极大值为
。当时，函数取得极小值为
。由数形结合可知
的实根个数为2。故C正确。
考点：用导数求极值。
练习册系列答案
相关题目
要做一个圆锥形的漏斗，其母线长为
，要使其体积为最大，则高为（ ）
A． | B． | C． | D． |
若函数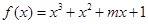
是R上的单调函数，则实数m的取值范围是（ ）。
A． | B． | C． | D．  |
函数
的单调递减区间为（ ）．
A． | B． | C． | D． |
函数
在区间
上单调递增，则实数
的取值范围是（ ）
A． | B． | C． | D． |
若
，其中
，则
( )
A． | B． | C． | D． |
函数f(x)＝ex－x(e为自然对数的底数)在区间[－1,1]上的最大值是( )
A．1＋ | B．1 | C．e＋1 | D．e－1 |
（2011•湖北）放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象称为衰变．假设在放射性同位素铯137的衰变过程中，其含量M（单位：太贝克）与时间t（单位：年）满足函数关系：M（t）=M0
，其中M0为t=0时铯137的含量．已知t=30时，铯137含量的变化率是﹣10In2（太贝克/年），则M（60）=（ ）
| A．5太贝克 | B．75In2太贝克 | C．150In2太贝克 | D．150太贝克 |
函数f(x)的定义域为R，f(－2)=2，对任意x∈R，xf′(x)＞－f(x)，则xf(x)＜－4的解集为（ ）
| A．(－2,2) | B．（－2，+∞） | C．（－∞，－2） | D．（－∞，+∞） |