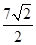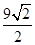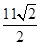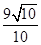题目内容
要做一个圆锥形的漏斗,其母线长为 ,要使其体积为最大,则高为( )
,要使其体积为最大,则高为( )
A. | B. | C. | D. |
D
解析试题分析:假设圆锥的高为 ,所以底面半径
,所以底面半径 .所以圆锥的体积表达式为
.所以圆锥的体积表达式为 .即
.即 ,所以由体积对高求导可得
,所以由体积对高求导可得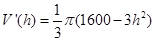 ,由
,由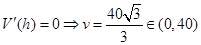 ,当
,当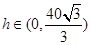 时,
时,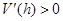 ,此时
,此时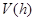 单调递增,当
单调递增,当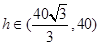 时,
时,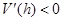 ,此时
,此时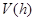 单调递减,所以
单调递减,所以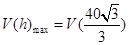 ,所以
,所以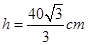 ,故选D.
,故选D.
考点:1.圆锥的体积公式.2.最值的求法.3.实际问题考虑定义域.

练习册系列答案
相关题目
已知 在R上开导,且
在R上开导,且 ,若
,若 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
函数 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
A.若函数在 时取得极值,则 时取得极值,则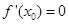 |
B.若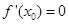 ,则函数在 ,则函数在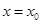 处取得极值 处取得极值 |
C.若在定义域内恒有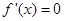 ,则 ,则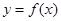 是常数函数 是常数函数 |
D.函数 在 在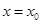 处的导数是一个常数 处的导数是一个常数 |
设函数 ,
, .若当
.若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设函数 在
在 上可导,则
上可导,则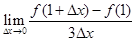 等于( )
等于( )
A.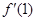 | B.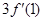 | C.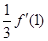 | D.以上都不对 |
方程x3﹣6x2+9x﹣4=0的实根的个数为( )
| A.0 | B.1 | C.2 | D.3 |
设f(x)=- x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>- | B.a<- | C.a> | D.不存在 |
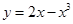 在横坐标为
在横坐标为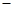 l的点处的切线为
l的点处的切线为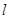 ,则点P(3,2)到直线
,则点P(3,2)到直线