题目内容
(本题满分13分)我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
炮兵阵地到目标的距离为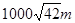 .
.
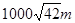 .
. 试题分析:在△ACD中,依题意可求得,∠CAD,利用正弦定理求得BD的长,进而在△ABD中,利用勾股定理求得AB.
解:在△ACD中,
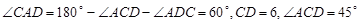
根据正弦定理有:
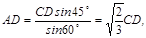
同理:在△BCD中,

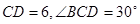 ,
,根据正弦定理有:
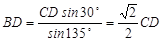 ,
, 在△ABD中,
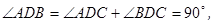 根据勾股定理有:
根据勾股定理有: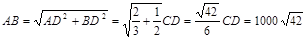 ,
,所以炮兵阵地到目标的距离为
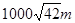 .………………………………13分
.………………………………13分点评:解决该试题的关键是在△ACD中,利用正弦定理求得BD的长,在△ABD中,利用勾股定理求得AB.

练习册系列答案
相关题目
 中,角
中,角 的对边分别是
的对边分别是 已知向量
已知向量
 ,且
,且 .
. 的大小;
的大小;  面积的最大值。
面积的最大值。 的面积
的面积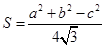 ,则
,则 =
=  ,
, 的最大值和最小正周期.,
的最大值和最小正周期., ABC的三个内角,若
ABC的三个内角,若 ,且C为锐角,求
,且C为锐角,求
 分别为
分别为 三个内角
三个内角 的对边,
的对边, ,(1)求
,(1)求 ; (2)若
; (2)若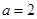 ,
, ;求
;求 .
.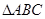 中,若
中,若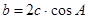 ,则这个三角形一定是( )
,则这个三角形一定是( )
 的半径是
的半径是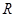 , 它的内接三角形
, 它的内接三角形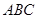 中, 有
中, 有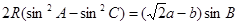 成立,求角
成立,求角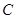 的大小及三角形面积
的大小及三角形面积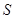 的最大值.
的最大值.