题目内容
【题目】设函数![]() ,其中
,其中![]() .
.
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的取值范围;
上的取值范围;
(2)若![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)当![]() 时,利用配方法可知当
时,利用配方法可知当![]() 时有最小值,当
时有最小值,当![]() 时有最大值.(2)由(1)知函数对称轴为
时有最大值.(2)由(1)知函数对称轴为![]() ,由此将
,由此将![]() 分成
分成![]() 两类,讨论函数的最大值,并使最大值小于或等于
两类,讨论函数的最大值,并使最大值小于或等于![]() ,由此求得实数
,由此求得实数![]() 的取值范围.(3)将问题转化为函数在区间
的取值范围.(3)将问题转化为函数在区间![]() 上的最小值和最大值之差的绝对值小于等于
上的最小值和最大值之差的绝对值小于等于![]() 来解决.对
来解决.对![]() 分成
分成![]() 四类,讨论函数的最值,并求得
四类,讨论函数的最值,并求得![]() 的取值范围.
的取值范围.
试题解析: ![]() ,所以
,所以![]() 在区间
在区间![]() 上单调减,在区间
上单调减,在区间![]() 上单调增,且对任意的
上单调增,且对任意的![]() ,都有
,都有![]() ,
,
(1)若![]() ,则
,则![]() .
.
![]() 在区间
在区间![]() 上的取值范围为
上的取值范围为![]() .
.
(2)“对任意的![]() ,都有
,都有![]() ”等价于“在区间
”等价于“在区间![]() 上,
上, ![]() ”.
”.
![]() 时,则
时,则![]() ,
,
所以![]() 在区间
在区间![]() 上单调减,在区间
上单调减,在区间![]() 上单调增.
上单调增.
当![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() ,
,
从而![]() .
.
当![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() ,
,
从而![]() .
.
综上, ![]() 的取值范围为区间
的取值范围为区间![]() .
.
(3)设函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,
,
所以“对任意的![]() ,都有
,都有![]() ”等价于“
”等价于“![]() ”.
”.
①当![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
从而![]() .
.
②当![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
从而![]() .
.
③当![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
从而![]() .
.
④当![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
从而![]() .
.
综上, ![]() 的取值范围为区间
的取值范围为区间![]() .
.

【题目】经统计,某医院一个结算窗口每天排队结算的人数及相应的概率如下:
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)求每天超过20人排队结算的概率;
(2)求2天中,恰有1天出现超过20人排队结算的概率.
【题目】下表提供了某厂生产某产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 2 | 4 | 6 | 8 | 10 |
| 4 | 5 | 7 | 9 | 10 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为: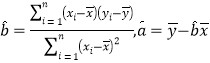 .
.