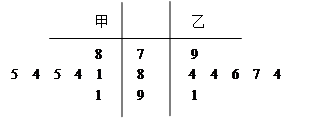题目内容
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
| 城市 | 民营企业数量 | 抽取数量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
(1)求
 、
、 的值;
的值;(2)若从城市A与B抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A的概率.
(1)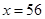 ,
,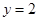 ;(2)
;(2)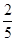 .
.
解析试题分析:本题主要考查分层抽样、随机事件的概率等基础知识,考查学生的分析问题解决问题的能力、计算能力、列举能力.第一问,利用分层抽样的解题方法,每一层的样本容量÷总容量都相等,列出方法,解出x,y的值;第二问,把城市A和B抽样的民营企业用字母表示出来,在6个中任取2个写出所有可能情况,一一列举出来,在其中选出符合题意的种数,再相除求概率.
(1)由题意得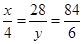 , 4分
, 4分
所以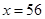 ,
,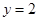 6分
6分
(2)记从城市A所抽取的民营企业分别为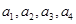 ,从城市B抽取的民营企业分别为
,从城市B抽取的民营企业分别为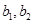 . 则从城市A、B抽取的6个中再随机选2个进行跟踪式调研的基本事件有
. 则从城市A、B抽取的6个中再随机选2个进行跟踪式调研的基本事件有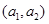 ,
,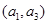 ,
,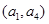 ,
,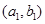 ,
,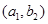 ,
,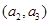 ,
, ,
,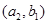 ,
,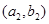 ,
,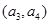 ,
,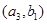 ,
,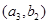 ,
,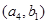 ,
,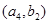 ,
,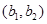 共15个 8分
共15个 8分
其中,来自城市A: 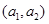 ,
,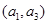 ,
,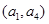 ,
,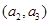 ,
, ,
,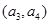 共6个 10分
共6个 10分
因此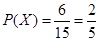 .故这2个都来自城市A的概率为
.故这2个都来自城市A的概率为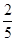 . 12分
. 12分
考点:分层抽样、随机事件的概率.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm)获得身高数据如下:
| 甲班: | 158 | 168 | 162 | 168 | 163 | 170 | 182 | 179 | 171 | 179 |
| 乙班: | 159 | 168 | 162 | 170 | 165 | 173 | 176 | 181 | 178 | 179 |
(1)完成数据的茎叶图(以百位十位为茎,以个位为叶),并求甲班样本数据的中位数、众数;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
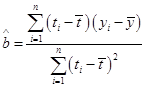 ,
,
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| | 支持A方案 | 支持B方案 | 支持C方案 |
| 35岁以下 | 200 | 400 | 800 |
| 35岁以上(含35岁) | 100 | 100 | 400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
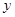 (万元)和房屋的面积
(万元)和房屋的面积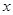 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知
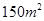 时的销售价格.
时的销售价格.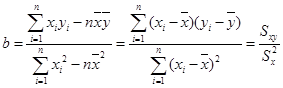
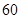 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过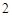 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过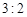 .
.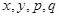 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).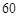 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定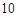 人,若需从这
人,若需从这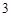 人进行问卷调查,设
人进行问卷调查,设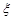 为选取的
为选取的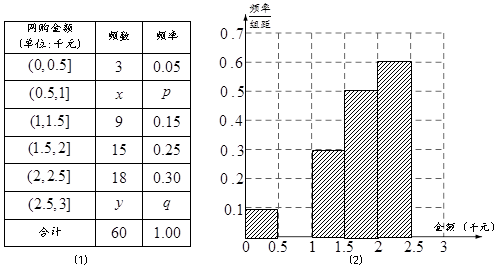
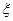 的分布列与期望.
的分布列与期望.