题目内容
【题目】已知函数f（x）=loga 
（a＞0且a≠1）是奇函数．
（1）求实数m的值；
（2）判断函数f（x）在区间（1，+∞）上的单调性并说明理由；
（3）当x∈（n，a﹣2）时，函数f（x）的值域为（1，+∞），求实数n，a的值．
【答案】
（1）解：根据题意，函数f（x）=loga
（a＞0且a≠1）是奇函数，
则有f（x）+f（﹣x）=0，
即loga +loga
=0，
则有loga（ ）（ ）=0，
即（ ）（ ）=1，
解可得：m=±1，
当m=1时，f（x）=loga
，没有意义，
故m=﹣1
（2）解：由（1）可得：m=﹣1，即f（x）=loga
，
设x1＞x2＞1，
f（x1）﹣f（x2）=loga
﹣loga
=loga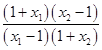
=loga（ 
），
又由x1＞x2＞1，
则0＜ ＜1，
当a＞1时，f（x1）﹣f（x2）＜0，则函数f（x）为减函数，
当0＜a＜1时，f（x1）﹣f（x2）＞0，则函数f（x）为增函数
（3）解：由（1）可得：m=﹣1，即f（x）=loga ，
其定义域为（﹣∞，﹣1）∪（1，+∞），
当n＜a﹣2＜﹣1时，有0＜a＜1，
此时函数f（x）为增函数，有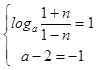 
，无解；
当1＜n＜a﹣2时，有a﹣2＞1，即a＞3，
此时函数f（x）为减函数，有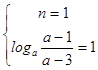 
，解可得a=2+ 
；
故n=1，a=2+
【解析】（1）根据题意，由函数奇偶性的性质可得f（x）+f（﹣x）=0，即loga 
+loga 
=0，结合对数的运算性质可得（ ）（ ）=1，解可得m的值，验证即可得答案；（2）由（1）可得函数的解析式，设x1＞x2＞1，结合对数的运算性质可得f（x1）﹣f（x2）=loga（ 
），分a＞1与0＜a＜1两种情况讨论f（x1）﹣f（x2）的符号，综合可得答案；（3）由（1）可得函数的解析式，进而求出函数f（x）的定义域，分n＜a﹣2＜﹣1和1＜n＜a﹣2两种情况讨论，求出a、n的值，即可得答案．
【考点精析】根据题目的已知条件，利用奇偶性与单调性的综合的相关知识可以得到问题的答案，需要掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．
