题目内容
设O为坐标原点,点M坐标为(3,2),若点N(x,y)满足不等式组
,当1≤s≤3时,则
•
的最大值的变化范围是( )
|
| OM |
| ON |
分析:先根据约束条件画出可行域,由于
•
=3x+2y,设z=3x+2y,再利用z的几何意义求最值,即可求解
| OM |
| ON |
解答: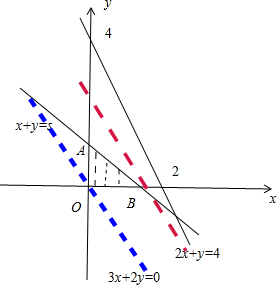 解:由于
解:由于
•
=(3,2)•(x,y)=3x+2y,
设z=3x+2y,则y=-
x+
z,将最大值转化为y轴上的截距最大
当1≤s≤2时,不等式组表示的平面区域如图(I)所示的阴影部分
作直线L:0=3x+2y,把L向可行域平移,结合图象可知,直线z=3x+2y经过点B(,s,0)时,z最大,
最大为:3s,此时,3s∈[3,6]
图(I)
当2<s≤3时,不等式组表示的平面区域如图(II)所示的阴影区域
直线z=3x+2y经过交点A(1,2)时,z最大,最大为:7.
作直线L:0=3x+2y,把L向可行域平移,结合图象可知,直线z=3x+2y经过点C时,z最大,
由
可得C(4-s,2s-4),此时z最大为:z=s+4∈(6,7]
此时,3s∈[3,6]
综上可得z的最大值的范围为[3,7],即则
•
的最大值的范围为[3,7],
故选B
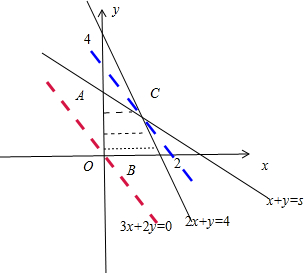
图(II)
 解:由于
解:由于| OM |
| ON |
设z=3x+2y,则y=-
| 3 |
| 2 |
| 1 |
| 2 |
当1≤s≤2时,不等式组表示的平面区域如图(I)所示的阴影部分
作直线L:0=3x+2y,把L向可行域平移,结合图象可知,直线z=3x+2y经过点B(,s,0)时,z最大,
最大为:3s,此时,3s∈[3,6]
图(I)
当2<s≤3时,不等式组表示的平面区域如图(II)所示的阴影区域
直线z=3x+2y经过交点A(1,2)时,z最大,最大为:7.
作直线L:0=3x+2y,把L向可行域平移,结合图象可知,直线z=3x+2y经过点C时,z最大,
由
|
此时,3s∈[3,6]
综上可得z的最大值的范围为[3,7],即则
| OM |
| ON |
故选B

图(II)
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
设O为坐标原点,点M(x,y)满足
,则z=2x+y的最大值为 ( )
|
| A、15 | B、5 | C、3 | D、-3 |
设O为坐标原点,点M坐标为(3,2),若点N(x,y)满足不等式组:
,当3≤s≤5时,则
•
的最大值的变化范围是( )
|
| OM |
| ON |
| A、[7,8] |
| B、[7,9] |
| C、[6,8] |
| D、[7,15] |