题目内容
如图,在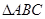 中,
中, ,
, ,
, 是
是 上的高,沿
上的高,沿 把
把 折起,使
折起,使 .
.
(Ⅰ)证明:平面 ⊥平面
⊥平面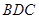 ;
;
(Ⅱ)若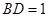 ,求三棱锥
,求三棱锥 的表面积.
的表面积.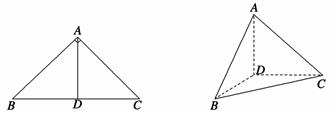
(Ⅰ)证明详见解析;(Ⅱ)  .
.
解析试题分析:(Ⅰ)先证线面垂直 平面
平面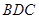 ,再证明面面垂直平面
,再证明面面垂直平面 平面
平面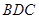 ;(Ⅱ)由第一问可知
;(Ⅱ)由第一问可知 都是直角三角形,可以求出
都是直角三角形,可以求出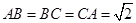 ,所以
,所以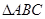 是等边三角形,分别求出四个三角形的面积.
是等边三角形,分别求出四个三角形的面积.
试题解析:(Ⅰ)因为折起前 是
是 边上的高.
边上的高.
所以当 折起后,
折起后, ,
,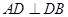 , 3分
, 3分
又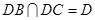 ,所以
,所以 平面
平面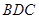 ,因为
,因为 平面
平面 ,
,
所以平面 平面
平面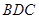 . 6分
. 6分
(Ⅱ)由(1)知,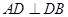 ,
, ,
,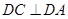 ,
,
因为 ,
,
所以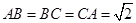 , 9分
, 9分
从而 ,
, ,
,
所以三棱锥 的表面积
的表面积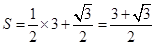 . 12分
. 12分
考点:1.线面垂直的判定;2.面面垂直的判定;3.三棱锥的表面积.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 ,
, ,
,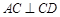 ,
,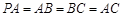 ,
, 是
是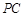 的中点.
的中点.
 ;
; 的平面角的正弦值.
的平面角的正弦值.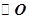 的直径,D为
的直径,D为 的中点,E为BC的中点.
的中点,E为BC的中点.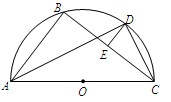
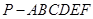 的底面是边长为1的正六边形,
的底面是边长为1的正六边形,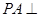 底面
底面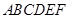 。
。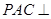 平面
平面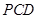 ;
;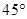 ,求三棱锥
,求三棱锥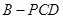 高的大小。
高的大小。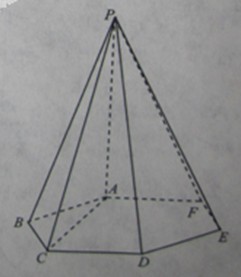
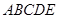 中,
中, 平面
平面 ,
,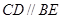 ,
,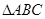 是等腰直角三角形,
是等腰直角三角形,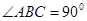 ,且
,且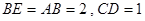 ,点
,点 是
是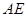 的中点.
的中点.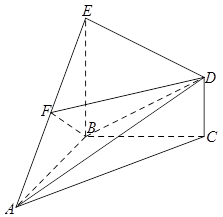
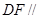 平面
平面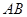 与平面
与平面 所成角的正弦值.
所成角的正弦值.  ,
,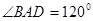 ,AD=AB=1,AC和BD交于O点.
,AD=AB=1,AC和BD交于O点.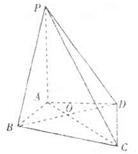
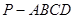 中,
中,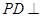 底面
底面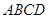 ,面
,面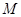 为侧棱
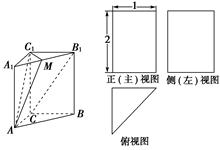
为侧棱 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 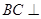 平面
平面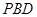 ;
; 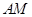 ∥平面
∥平面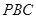 ;
; 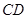 上是否存在点
上是否存在点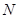 ,使
,使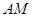 与
与 所成角的余弦值为
所成角的余弦值为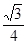 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点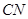 的长;若不存在,说明理由.
的长;若不存在,说明理由.
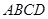 中,
中,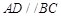 ,
,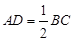 ,
,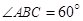 ,
, 是
是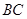 的中点.将梯形
的中点.将梯形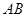 旋转
旋转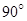 ,得到梯形
,得到梯形 (如图).
(如图).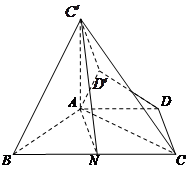
 平面
平面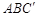 ;
; 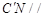 平面
平面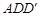 ;
;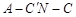 的余弦值.
的余弦值.