题目内容
【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且与直线x﹣y+1=0相交的弦长为2 ![]() ,求圆的方程.
,求圆的方程.
【答案】解:设所求圆的圆心为(a,b),半径为r, ∵点A(2,3)关于直线x+2y=0的对称点A′仍在这个圆上,
∴圆心(a,b)在直线x+2y=0上,
∴a+2b=0,①
(2﹣a)2+(3﹣b)2=r2 . ②
又直线x﹣y+1=0截圆所得的弦长为2 ![]() ,
,
圆心(a,b)到直线x﹣y+1=0的距离为d= ![]() =
= ![]() ,
,
则根据垂径定理得:r2﹣( ![]() )2=(
)2=( ![]() )2③
)2③
解由方程①、②、③组成的方程组得: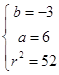 或
或 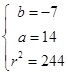
∴所求圆的方程为(x﹣6)2+(y+3)2=52或(x﹣14)2+(y+7)2=244
【解析】设出圆的方程为(x﹣a)2+(y﹣b)2=r2 , 由圆上的点关于直线的对称点还在圆上得到圆心在这条直线上,设出圆心坐标,代入到x+2y=0中得到①;把A的坐标代入圆的方程得到②;由圆与直线x﹣y+1=0相交的弦长为2 ![]() ,利用垂径定理得到弦的一半,圆的半径,弦心距成直角三角形,利用勾股定理得到③,三者联立即可求出a、b和r的值,得到满足题意的圆方程.
,利用垂径定理得到弦的一半,圆的半径,弦心距成直角三角形,利用勾股定理得到③,三者联立即可求出a、b和r的值,得到满足题意的圆方程.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目