题目内容
(本小题满分14分)
已知函数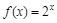 ,
,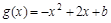
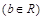 ,记
,记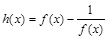 。
。
(Ⅰ)判断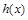 的奇偶性,并证明;
的奇偶性,并证明;
(Ⅱ)对任意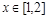 ,都存在
,都存在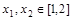 ,使得
,使得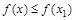 ,
,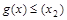 .若
.若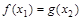 ,求实数
,求实数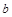 的值;
的值;
(Ⅲ)若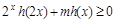 对于一切
对于一切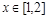 恒成立,求实数
恒成立,求实数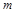 的取值范围.
的取值范围.
已知函数
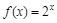 ,
,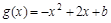
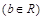 ,记
,记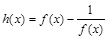 。
。(Ⅰ)判断
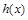 的奇偶性,并证明;
的奇偶性,并证明;(Ⅱ)对任意
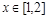 ,都存在
,都存在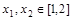 ,使得
,使得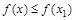 ,
,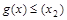 .若
.若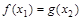 ,求实数
,求实数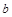 的值;
的值;(Ⅲ)若
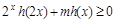 对于一切
对于一切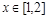 恒成立,求实数
恒成立,求实数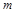 的取值范围.
的取值范围.(1)奇函数(2)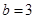 (3)
(3)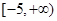
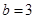 (3)
(3)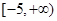
试题分析:解:(Ⅰ)函数
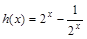 为奇函数………………………………………………2分
为奇函数………………………………………………2分现证明如下:
∵函数
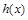 的定义域为
的定义域为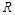 ,关于原点对称。……………………………………3分
,关于原点对称。……………………………………3分由
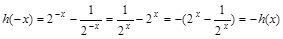 …………………5分
…………………5分∴函数
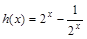 为奇函数…………………………………………………6分
为奇函数…………………………………………………6分(Ⅱ)据题意知,当
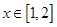 时,
时,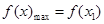 ,
,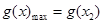 …………7分
…………7分∵
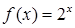 在区间
在区间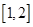 上单调递增,
上单调递增,∴
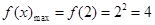 ,即
,即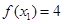 ………………………………………8分
………………………………………8分又∵
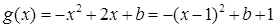
∴函数
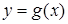 的对称轴为
的对称轴为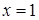
∴函数
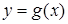 在区间
在区间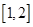 上单调递减
上单调递减∴
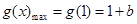 ,即
,即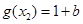 ………………………………………9分
………………………………………9分由
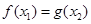 ,
,得
 ,∴
,∴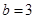 ………………………………………………………………10分
………………………………………………………………10分(Ⅲ)当
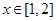 时,
时,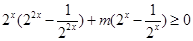
即
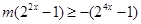 ,
,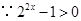 ,
,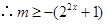 …………………………………………………12分
…………………………………………………12分令
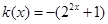 ,
,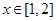
下面求函数
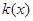 的最大值。
的最大值。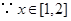 ,
,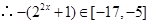
∴
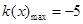 ……………………………………………………………………13分
……………………………………………………………………13分故
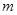 的取值范围是
的取值范围是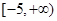 ………………………………………………………14分
………………………………………………………14分 点评:解决该试题的关键是能熟练的运用指数函数和二次函数的性质得到最值,以及根据奇偶性的定义准确的证明,同时对于不等式的恒成立问题,能分离参数法来得到其取值范围。属于中档题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
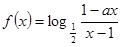 为奇函数,a为常数。
为奇函数,a为常数。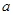 的值;并证明
的值;并证明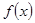 在区间
在区间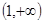 上为增函数;
上为增函数;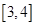 上的每一个
上的每一个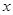 的值,不等式
的值,不等式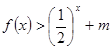 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.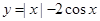 的图象大致是
的图象大致是 
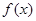 的定义域为
的定义域为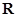 ,满足
,满足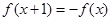 ,且当
,且当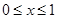 时,
时,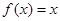 ,
,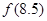 等于( )
等于( )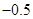
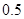
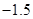
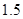
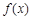 有( ).
有( ).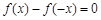
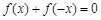
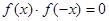

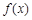 是定义在R上的奇函数,当
是定义在R上的奇函数,当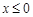 时,
时,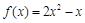 ,则
,则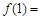
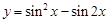 的最小正周期为 .
的最小正周期为 .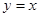
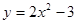
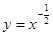
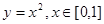
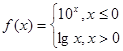 ,则
,则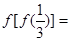 .
.